2052

Stała pitagorejska √2

Wartość odpowiadająca wielkości przekątnej kwadratu o boku długości 1. Wynosi w przybliżeniu 1,414. Można ją uważać za jeden z najstarszych przykładów liczb niewymiernych (nie można jej wyrazić w postaci ułamkowej jako stosunku dwóch liczb).

Z liczbą √2 spotykamy się, pracując z jakimkolwiek dokumentem drukowanym. Stosunki wielkości boków w powszechnie stosowanych formatach arkuszy wynoszą bowiem właśnie 1:√2. Stosunek ten jest często określany „bramą harmonii“ i jest ściśle związany z inną słynną stałą – złotym podziałem.

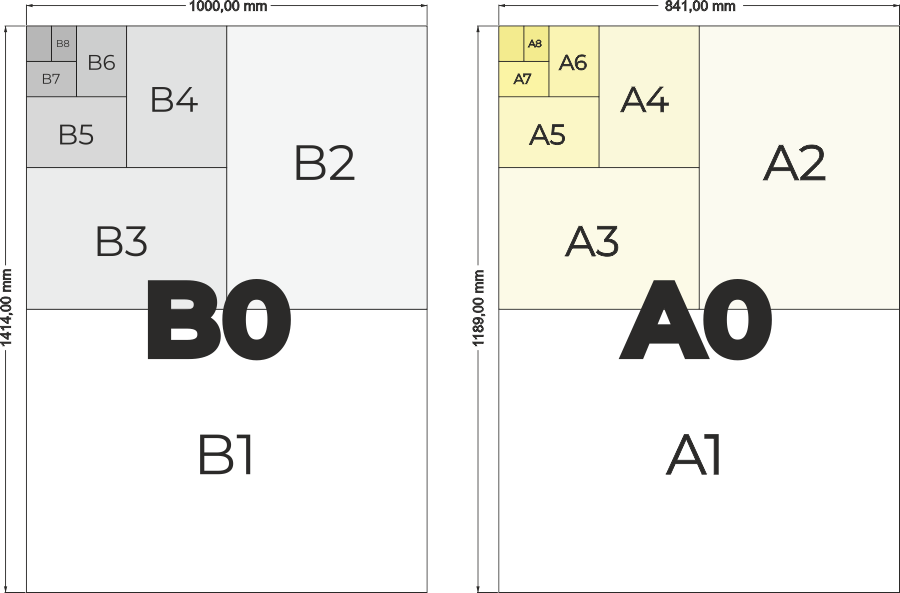
Szereg A to podstawowe formaty A₀, którego powierzchnia ma wielkość 1 m², a stosunek wielkości boków wynosi 1: √2. Kolejne formaty (A1, A2, A3, A4,…) uzyskujemy każdorazowo w wyniku podziału na pół dłuższego boku.

Szereg B to podstawowy format B_0, a długość krótszego boku papieru ma 1 m. Stosunek wielkości boków wynosi również 1: √2, czyli format B₀ ma powierzchnię wynoszącą 1,4142 m².

Złoty podział ϕ

Złoty podział, zwany także boską proporcją, oznaczamy grecką literą ϕ. To jedna z ważnych i istotnych stałych matematycznych, która znacznie wykracza poza granice matematyki. Ponoć wykorzystywali ją już Egipcjanie, kiedy budowali piramidy.

Złoty podział, inaczej złota proporcja, to stosunek 1,618. Uznaje się, że podział odcinka właśnie w tym stosunku jest najbardziej przyjazny dla naszych oczu. To dlatego na puszce lub kartonie z napojem logo nie jest umieszczone pośrodku, ale właśnie w stosunku złotego podziału, czyli gdzieś w górnej jednej trzeciej wysokości. W sztuce i fotografii złoty podział jest uważany za idealną proporcję między różnymi długościami. Używa się aproksymacji jednej trzeciej, która jest przy robieniu zdjęć wystarczająca.

 

Liczba Eulera e

Ludolfina czy stała pitagorejska są znane od czasów starożytności, natomiast liczba Eulera e jest o wiele młodsza. Pojawiła się dopiero wraz z nadejściem oprocentowania złożonego (wyznacza graniczny roczny zysk z jednostki przy rocznym stuprocentowym oprocentowaniu). Jej przybliżona wartość wynosi 2,718 i została nazwana nazwiskiem szwajcarskiego matematyka i fizyka Leonharda Eulera (1707-1783). Dziś to ważna stała o dużym znaczeniu nie tylko w matematyce, ale też w innych naukach przyrodniczych, na przykład astronomii czy fizyce.

Jedną z ważnych właściwości liczby Eulera jest to, że jest podstawą logarytmu naturalnego. Ma on swój specyficzny zapis ln (x) i obowiązuje zasada, że: ln(x)=y ⇔ e^y =x

Liczba Eulera stosowana jest do obliczania granic, pochodnych i całek. Z liczbą pi pojawia się we wzorze tożsamości Eulera, który kiedyś uznano za najpiękniejszy wzór matematyczny.

 

Ludolfina

Określa stosunek obwodu koła do długości jego średnicy. Wykorzystywana jest w dziesiątkach równań i większość ludzi zna jej przybliżoną wartość 3,14.

Liczba pi ma jednak nieskończone dziesiętne rozwinięcie. Archimedes jako pierwszy próbował jak najdokładniej je ustalić. Rozważał on ciąg wielokątów opisanych na okręgu i wpisanych w okrąg. Liczba ich boków wciąż rosła, a tym samym coraz bardziej i bardziej zbliżała się do długości okręgu, co precyzowało obliczenie liczby pi.

Identyczny sposób co Archimedes zastosował w XVI wieku holenderski matematyk Ludolph van Ceulen, który mniej więcej 25 lat swojego życia poświęcił na obliczanie liczby pi. Za pomocą foremnego 4 611 686 018 427 387 904-kąta liczbę pi obliczył z dokładnością do 35 miejsc po przecinku. Na jego cześć liczbę pi nazywa się także ludolfiną.

 

Rachunek różniczkowy i całkowy

• Powstanie i rozwój metod różniczkowych i całkowych – różniczkowania, całkowania i sumowania zbieżnych nieskończonych szeregów – należy do najwybitniejszych osiągnięć matematyki XVII wieku.
• Rachunek różniczkowy odkryło jednocześnie dwóch wielkich naukowców – Isaac Newton w Anglii i Gottfried Wilhelm Leibniz w Niemczech. Obaj tak naprawdę doszli do identycznych wyników, ale każdy swoją drogą. Newton rachunek różniczkowy i całkowy opracował pierwszy, ale Leibniz pierwszy opublikował swoje wnioski.
• Newton zajmował się przede wszystkim stopniem zmiany prędkości w danym odcinku czasu. Na jego koncepcje funkcji i ich pochodnych miała więc duży wpływ teoria fizyki i mechaniki. Także wielkości matematyczne rozumiał jako wielkości fizyczne zmieniające się w niezależnie płynącym czasie nieograniczonym ruchem w nieograniczonej przestrzeni.
• Leibniz bazował zaś na dwóch podstawowych zadaniach matematyki: znaleźć równanie stycznej do krzywej i obliczyć pole powierzchni ograniczonej krzywą. Wprowadził on swoje oznaczenia, których używamy do tej pory. Symbol dla całki jako literę początkową słowa summa (suma), literę  dla oznaczenia różniczkowania jako pierwszą literę słowa differenita (różnica).
• Całkę rozumiał jako sumę nieskończenie wielu małych „różnic“. Powierzchnię pod krzywą wypełnił coraz mniejszymi prostokątami, których pole potrafił obliczyć. Prostokąty te wciąż pomniejszał, aż były nieskończenie małe. Ich powierzchnię następnie zsumował (zsumowanie wszystkich powierzchni nazywamy całkowaniem).