Pythagorean constant √2
Is the value corresponding to the diagonal size of the unit square. It is approximately 1,414. It can be considered as one of the oldest examples of irrational numbers (which cannot be expressed as a fraction of two numbers).
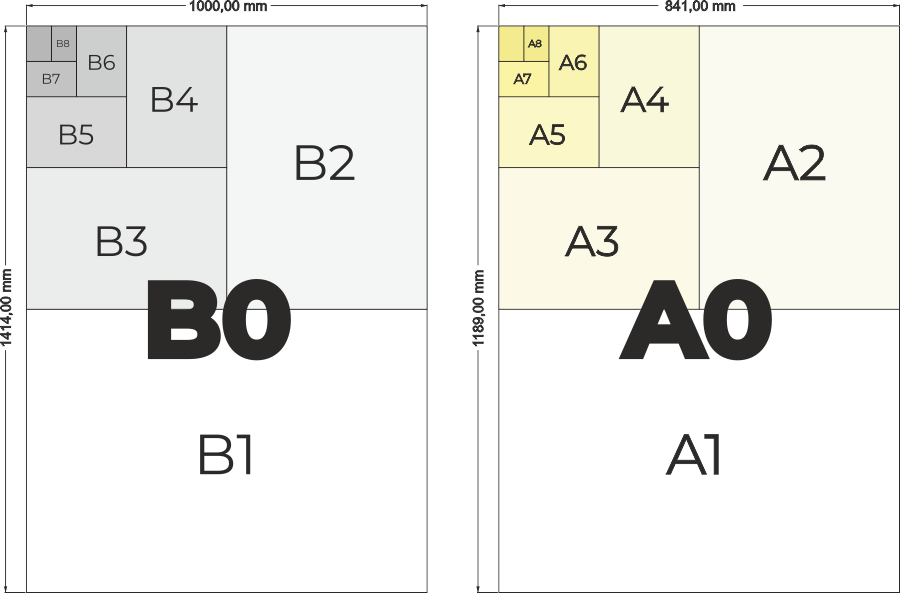
The number √2 is encountered when working with any printed document. The aspect ratios of commonly used paper sizes are exactly 1: √2. This ratio is often referred to as the „gate of harmony“ and is closely related to another famous constant – the golden ratio.
Series A is defined by the basic format A0, whose area is 1 m2 and the aspect ratio is 1: √2. Other formats (A1, A2, A3, A4, …) are always obtained by halving the longer side.
Series B is defined by the basic format B0 and the length of the shorter side of the paper 1 m. The aspect ratio is then again 1: √2, so the B0 format has an area of 1.4142 m2.
Golden ratio ϕ
The golden ratio, sometimes also a divine relationship, is denoted by the Greek letter ϕ. It is one of the important and remarkable mathematical constants that goes well beyond mathematics. It is said to have been used by the Egyptians to build the pyramids.
The golden ratio is called the ratio of 1,618: 1. It is said that the division of the line in this ratio is most pleasing to our eyes. That is why e.g. on the can or box of the drink, the logo is not placed in the middle, but in the location corresponding to the golden ratio, ie somewhere in the upper third of the height. In art and photography, the golden ratio is considered to be the ideal proportion between different lengths. An approximation of one third is used, which is sufficient when shooting photographs or films.
Euler’s number e
While Ludolph’s number or Pythagorean constant has been known since ancient times, Euler’s number e is much younger and does not appear until the advent of a compound interest rate calculations (it sets a limiting annual return on a unit amount at one hundred percent annual interest). Its approximate value is 2,718 and it was named after the Swiss mathematician and physicist Leonhard Euler (1707 – 1783). Today, it is an important constant of great importance not only for mathematics, but also for other natural sciences, such as astronomy or physics.
One of the important properties of the Euler number is that it is the basis of the natural logarithm. It has its specific notation ln (x) and holds that: ln (x) = y ⇔ ey = x
Euler’s number is useful in that it appears in the calculation of limits, derivatives and integrals. The number Pi appears in Euler’s identity formula ![]() , which was once voted the most beautiful mathematical relationship.
, which was once voted the most beautiful mathematical relationship.
Ludolf’s number p
indicates how many times the circumference of the circle is larger than its diameter. It is used in dozens of equations and most people know its approximate value as 3.14.
However, the number p (pi) has an infinite decimal development, and Archimedes was the first trying to determine it as accurately as possible. He proceeded by inserting a circle and copying polygons. The number of their sides was constantly increasing, thus getting closer and closer to the shape of the circle and thus refining the calculation of the number pi.
The same procedure as Archimedes was used in the 16th century by the Dutch mathematician Ludolph van Ceulen, who spent about 25 years of his life counting the number pi. He calculated the number pi to 35 decimal places using a regular 4,611,686,018,427,387,904,904-polygon. In his honor, the number Pi is today also called Ludolf’s number.
Infinitesimal count
- The birth and development of infinitesimal methods – methods of derivation, integration and addition of convergent infinite series, are among the most remarkable results of 17th century mathematics.
- Infinitesimal calculus was discovered simultaneously by two great scientists – Isaac Newton in England and Gottfried Wilhelm Leibniz in Germany. They both basically got the same results, only each went their own way. Newton first invented the calculus, but Leibniz was the first to publish his conclusions.
- Newton was primarily concerned with the rate of speed change over time. His conception of functions and their derivatives is thus strongly influenced by physical-mechanical theory. He also understands mathematical quantities as physical quantities that change in an independently flowing time by unrestricted continuous motion in unbounded space.
- Leibniz bases the introduction of the calculus on two basic mathematical problems: finding the equation of the tangent to the curve, and calculating the area bounded by the curve. For the infinitesimal calculus he introduced the terminology that we basically use today. The character for the integral as the initial letter of the word summa (sum), the letter d for the designation of derivation as the first letter of the word differenita (difference).
The integral was understood by Leibniz as the sum of infinitely many, infinitesimally small quantities. He filled the area under the curve with smaller and smaller rectangles, for which he could calculate the area. He kept thinning these rectangles until they were infinitely small. Their area was then summed (summing all these areas we call integration).





