2052

Konstante von Pythagoras √2

Wert, der der Größe der Diagonale eines Einheitsquadrats entspricht. Er beträgt etwa 1,414. Die Konstante von Pythagoras kann als eines der ältesten Beispiele irrationaler Zahlen (diese können nicht durch einen Bruch als Quotient zweier Zahlen ausgedrückt werden) betrachtet werden.

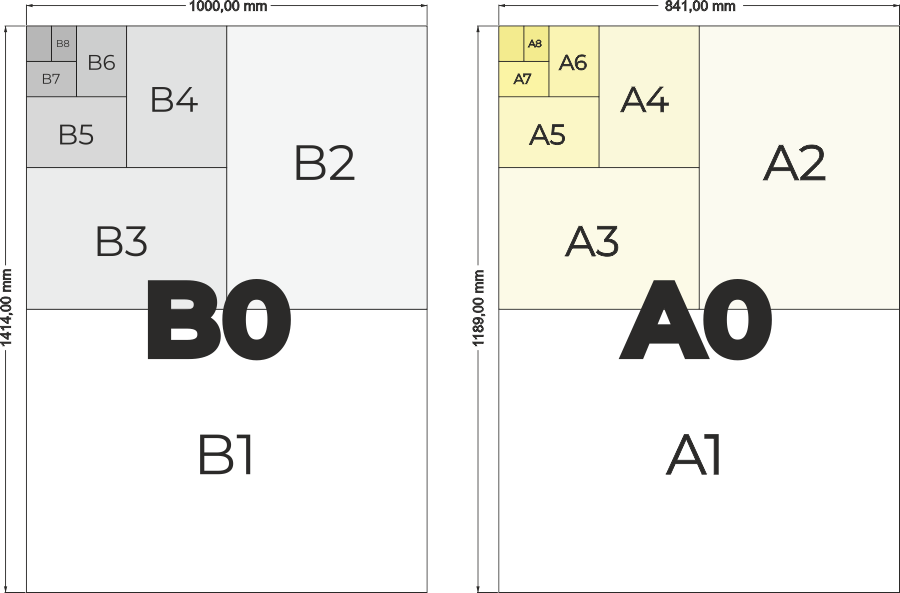
Auf die Zahl √2 stoßen wir bei der Arbeit mit jedem gedruckten Dokument. Die Verhältnisse der Seitengrößen bei den üblich genutzten Papierformaten sind nämlich gerade 1: √2. Dieses Verhältnis wird im Tschechischen auch als „Tor zur Harmonie“ bezeichnet und steht eng mit einer weiteren berühmten Konstante in Zusammenhang – dem Goldenen Schnitt.

Die A-Reihe wird durch das Grundformat A0 definiert, dessen Fläche eine Größe von 1 m² hat, und das Verhältnis der Seitengrößen beträgt 1: √2. Die weiteren Formate (A1, A2, A3, A4, …) erhalten wir stets durch Halbieren der längeren Seite.

Die B-Reihe wird durch das Grundformat B0 und die Länge der kürzeren Papierseite von 1 m definiert. Das Verhältnis der Seitengrößen beträgt wiederum 1: √2. Das Format B0 hat also einen Flächeninhalt von 1,4142 m².

 

Goldener Schnitt ϕ

Der Goldene Schnitt, manchmal auch als göttliche Teilung bezeichnet, wird mit dem griechischen Buchstaben ϕ gekennzeichnet. Es handelt sich um eine bedeutende und beachtenswerte mathematische Konstante, die die Grenzen der Mathematik deutlich überschreitet. Angeblich wurde sie bereits von den Ägyptern beim Pyramidenbau genutzt.

Als Goldener Schnitt wird das Verhältnis von 1,618 : 1 bezeichnet. Es heißt, dass die Teilung einer Strecke gerade in diesem Verhältnis am harmonischsten für unser Auge ist. Gerade deshalb befindet sich z. B. auf einer Getränkedose oder einem Getränkekarton das Logo nicht in der Mitte, sondern gerade im Verhältnis des Goldenen Schnittes, also irgendwo im oberen Drittel der Höhe. In der Kunst und der Fotografie gilt der Goldene Schnitt als ideale Proportion zwischen verschiedenen Längen. Es wird die Approximation von einem Drittel genutzt, die beim Fotografieren ausreichend ist.

 

Eulersche Zahl e

Während die Ludolphsche Zahl oder die Konstante von Pythagoras bereits seit dem Altertum bekannt sind, ist die Eulersche Zahl e weitaus jünger und tritt erst mit dem Aufkommen der Beziehung für die Zinseszinsrechnung auf (sie bestimmt den Limit-Jahresrückfluss eines Einheitsbetrags bei hundertprozentigem Jahreszins). Ihr annähernder Wert beträgt 2,718 und sie wurde nach dem Schweizer Mathematiker und Physiker Leonhard Euler (1707 – 1783) benannt. Heute handelt es sich um eine wichtige Konstante, die nicht nur für die Mathematik von großer Bedeutung ist, sondern auch für weitere Naturwissenschaften, zum Beispiel für die Astronomie oder die Physik.

Eine wichtige Eigenschaft der Eulerschen Zahl ist, dass es sich um die Basis des natürlichen Logarithmus handelt. Dieser hat seine spezifische Darstellung ln (x) und es gilt, dass: ln(x)=y ⇔ e^y =x

Die Eulersche Zahl ist nützlich, da sie bei der Berechnung von Grenzwerten, Ableitungen und Integralen auftaucht. Zusammen mit der Kreiszahl Pi taucht sie in der Formel der Eulerschen Identität auf, die einst zur schönsten mathematischen Beziehung gewählt wurde.

 

Ludolphsche Zahl

Die Ludolphsche Zahl gibt an, wievielmal der Umfang eines Kreises größer ist, als sein Durchmesser. Sie wird in Dutzenden Gleichungen genutzt und die meisten Menschen kennen ihren ungefähren Wert 3,14.

Die Kreiszahl Pi hat jedoch eine unendliche Dezimalentwicklung. Als erster versuchte Archimedes sie so genau wie möglich zu bestimmen. Er ging so vor, dass er Inkreise und Umkreise von Vielecken bildete. Er steigerte die Seitenzahl der Vielecke ständig und näherte sich so immer mehr der Form eines Kreises, wodurch er auch die Berechnung der Kreiszahl Pi präzisierte.

Dasselbe Verfahren wie Archimedes nutzte im 16. Jahrhundert der niederländische Mathematiker Ludolph van Ceulen und er verbrachte etwa 25 Jahre seines Lebens mit der Berechnung der Kreiszahl Pi.  Er berechnete die Zahl Pi mit Hilfe eines regelmäßigen 4 611 686 018 427 387 904-ecks auf 35 Nachkommastellen. Ihm zu Ehren wird die Zahl Pi auch als Ludolphsche Zahl bezeichnet.

 

Infinitesimalrechnung

• Die Genese und Entwicklung infinitesimaler Methoden – die Methoden der Differenziation, Integration und Addition konvergenter unendlicher Reihen – gehört zu den beachtenswertesten Ergebnissen der Mathematik des 17. Jahrhunderts.
• Die Infinitesimalrechnung entdeckten gleichzeitig zwei große Wissenschaftler – Isaac Newton in England und Gottfried Wilhelm Leibniz in Deutschland. Beide kamen im Prinzip zu denselben Ergebnissen, nur ging jeder seinen eigenen Weg. Newton entdeckte das Kalkül als Erster, aber Leibniz publizierte seine Schlüsse als Erster.
• Newton beschäftigte sich primär mit dem Maß der Geschwindigkeitsänderung in einem gegebenen Zeitabschnitt. Sein Konzept der Funktionen und ihrer Ableitungen wird also stark von der physikalisch-mechanischen Theorie beeinflusst. Auch mathematische Größen versteht er als physikalische Größen, die sich in unabhängig vergehender Zeit durch unbeschränkte kontinuierliche Bewegung in einem unbegrenzten Raum verändern.
• Leibniz geht bei der Einführung des Kalküls von zwei Grundaufgaben der Mathematik aus: die Gleichung der Tangente zur Kurve zu finden und den Inhalt der von der Kurve begrenzten Flächen zu berechnen. Für die Infinitesimalrechnung führt er die Terminologie ein, die wir im Wesentlichen bis heute verwenden. Das Zeichen für das Integral als Anfangsbuchstabe des Wortes summa (Summe), den Buchstaben  zur Kennzeichnung der Differenziation als erster Buchstabe des Wortes differenita (Differenz).
• Das Integral verstand er als Summe unendlich vieler unendlich kleiner Größen. Die Fläche unter der Kurve füllte er mit immer kleineren Rechtecken, bei denen er den Flächeninhalt berechnen konnte. Diese Rechtecke machte er immer schmaler, bis sie unendlich klein waren. Ihre Flächen wurden dann addiert (die Addition aller Flächen nennt man Integration).