Pythagorova konstanta √2
Hodnota odpovídající velikosti úhlopříčky jednotkového čtverce. Činí přibližně 1,414. Lze ji považovat za jeden z nejstarších příkladů iracionálních čísel (nelze je vyjádřit zlomkem jako podíl dvou čísel).
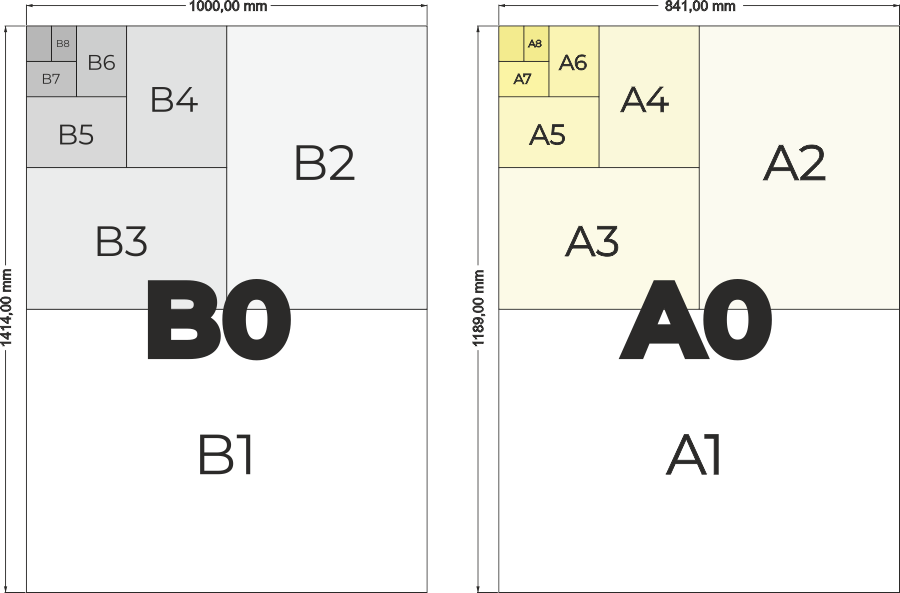
S číslem √2 se setkáváme při práci s jakýmkoliv tištěným dokumentem. Poměry velikostí stran u běžně používaných formátů papíru jsou totiž právě 1: √2. Tento poměr je často označování jako „brána harmonie“ a úzce souvisí s další slavnou konstantou – zlatým řezem.
Řada A je definována základním formátem A0, jehož plocha má velikost 1 m2 a poměr velikostí stran je 1: √2 . Další formáty (A1, A2, A3, A4,…) získáme vždy půlením delší strany.
Řada B je definována základním formátem B0 a délkou kratší strany papíru 1 m. Poměr velikostí stran je pak opět 1: √2 , čili formát B0 má plochu o velikosti 1,4142 m2.
Zlatý řez φ
Zlatý řez, někdy též božský poměr, značíme řeckým písmenem φ. Jedná se o jednu z významných a pozoruhodných matematických konstant, která výrazně přesahuje hranice matematiky. Údajně ji využívali již Egypťané při stavbě pyramid.
Zlatým řezem se nazývá poměř 1, 618: 1. Traduje se, že rozdělení úsečky právě v tomto poměru nejvíce lahodí našim očím. Právě proto např. na plechovce či krabici od nápoje není logo umístěno uprostřed, ale právě v poměru zlatého řezu, tedy někde v horní třetině výšky.
V umění a fotografii je zlatý řez pokládán za ideální proporci mezi různými délkami. Používá se aproximace jedné třetiny, která je při fotografování dostačující.
Eulerovo číslo e
Zatímco Ludolfovo číslo nebo Pythagorova konstanta jsou známy již od dávného starověku, Eulerovo číslo e je daleko mladší a objevuje se až s příchodem vztahu pro složené úrokování (stanovuje limitní roční návratnost jednotkové částky při ročním stoprocentním úroku). Jeho přibližná hodnota je 2,718 a bylo pojmenováno bylo podle švýcarského matematika a fyzika Leonharda Eulera (1707 – 1783). Dnes se jedná o důležitou konstantu s velkým významem nejen pro matematiku, ale i další́ přírodní vědy, například astronomii nebo fyziku.
Jednou z důležitých vlastností Eulerova čísla je, že se jedná o základ přirozeného logaritmu. Ten má svůj specifický zápis ln (x) a platí, že: ln(x)=y ⇔ ey =x
Eulerovo číslo je užitečné v tom, že se objevuje při výpočtu limit, derivací a integrálů. S číslem Pí se objevuje ve vzorci Eulerovi identity, ![]() který byl kdysi zvolen za nejkrásnější matematický vztah.
který byl kdysi zvolen za nejkrásnější matematický vztah.
Ludolfovo číslo
udává, kolikrát je obvod kruhu větší než jeho průměr. Využívá se v desítkách rovnic a většina lidí zná jeho přibližnou hodnotu jako 3,14.
Číslo pí má však nekonečný desetinný rozvoj a stanovit jej co nejpřesněji zkoušel jako první Archimedes. Ten postupoval tak, že kružnici vepisoval a opisoval mnohoúhelníky. Počet jejich stran neustále zvyšoval a tím se stále více a více přibližoval tvaru kružnice a tím i zpřesňoval výpočet čísla pí.
Stejný postup jako Archimedes použil v 16. století holandský matematik Ludolph van Ceulen a přibližně 25 let svého života trávil počítáním čísla pí. Dopočítal pomocí pravidelného 4 611 686 018 427 387 904-úhelníku číslo pí na 35 desetinných míst. Na jeho počest se číslo Pí nazývá také Ludolfovo číslo.
Infinitezimální počet
- Zrod a rozvoj infinitezimálních metod – metod derivování, integrování a sčítání konvergentních nekonečných řad patří k nejpozoruhodnějším výsledkům matematiky 17. století.
- Infinitezimální počet objevili současně dva velcí vědci – Isaac Newton v Anglii a Gottfried Wilhelm Leibniz v Německu. Oba v podstatě došli ke stejným výsledkům, jen každý šel svou vlastní cestou. Newton kalkul objevil první, ale Leibniz své závěry první publikoval.
- Newton se primárně zabýval mírou změny rychlosti za daný časový úsek. Jeho koncepce funkcí a jejich derivací je tedy silně ovlivněna fyzikálně-mechanickou teorií. I






