In addition to mathematics, the parabolic curve is also present in physics, astronomy, wireless communications, industry, solar energy, engineering, and even optical illusions.
V – vertex
F – Focus
Applications of parabolic curves often require specific curve information, including focus.
Why are we interested in the location of the focus of the dish?
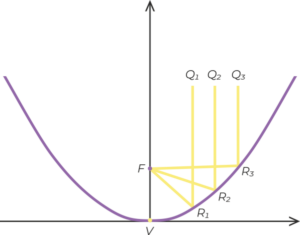
Parabolic reflector is a curved surface with a cross-section of parabolic shape, used to direct light or sound waves.
Any light or sound waves entering the parabola parallel to the axis of the parabola and impinging on the inner surface of the parabola are reflected back to the focus.
Radio telescope antennas and satellite dishes use this concept by placing the receiver in focus to obtain a concentrated signal.
In a similar way, the parabolic reflector in the lamp concentrates the light emitted by the bulb placed in the focus into a directed beam of light.
The same principle works in the headlights of your car and in the light cannons.
Where the waves have been received by a parabola, the parabolic reflector in the lamp directs the light waves outwards.
Other applications of parabolic curves:
A well-known example of a parabola in physics is the trajectory of a particle or body in motion under the influence of gravity (without air resistance).
Such a trajectory is always an approximation of a parabola and was discovered in the early 17th century by Galileo.
Suspension bridge: the parabola represents the profile of the suspension bridge ropes.
Arch bridge: the parabola represents the profile of the supporting structure of the arch bridge. This concrete bridge transfers its weight horizontally to the supports.





