Kromě matematiky je parabolická křivka přítomna i ve fyzice, astronomii, bezdrátové komunikaci, průmyslu, sluneční energii, strojírenství a dokonce i v optických iluzích.
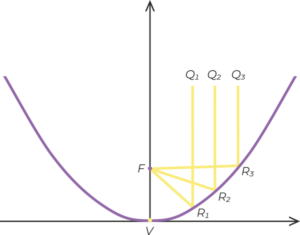
V – vrchol
F – Ohniště
Aplikace parabolických křivek často vyžadují specifické informace o křivce včetně ohniska.
Proč nás zajímá umístění ohniska paraboly?
Parabolický reflektor je zakřivený povrch s tvarem průřezu paraboly používaný k usměrňování světelných nebo zvukových vln.
Jakékoli světelné nebo zvukové vlny vstupující do paraboly rovnoběžně s osou paraboly a dopadající na vnitřní povrch paraboly se odrážejí zpět do ohniska.
Antény radioteleskopů a satelitní paraboly používají tento koncept umístěním přijímače do ohniska, aby se získal koncentrovaný signál.
Podobným způsobem parabolický reflektor ve svítilně koncentruje světlo vyzařované žárovkou, umístěnou v ohnisku, do směrovaného paprsku světla.
Stejný princip funguje ve světlometech vašeho auta a v reflektorech.
Tam, kde byly zvukové vlny přijímány parabolou, parabolický reflektor ve svítilně směřuje světelné vlny ven.
Další aplikace parabolických křivek:
Dobře známý příklad paraboly ve fyzice je trajektorie částice nebo tělesa v pohybu pod vlivem gravitace (bez odporu vzduchu).
Taková dráha je vždy aproximací paraboly a byla objevena na počátku 17. století Galileem.
Visutý most: parabola představuje profil lana visutého mostu.
Obloukový most: parabola představuje profil nosné konstrukce obloukového mostu.
Tento betonový most přenáší svou váhu vodorovně do opěr.





