Neben der Mathematik ist die Parabelkurve auch in der Physik, der Astronomie, der drahtlosen Kommunikation, der Industrie, der Sonnenenergie, dem Maschinenbau und sogar bei optischen Illusionen anwesend.
V – Scheitelpunkt
F – Brennpunkt
Die Anwendungen parabolischer Kurven erfordern häufig spezifische Informationen zur Kurve, inkl. Brennpunkt.
Warum interessiert uns die Position des Brennpunkts einer Parabel?
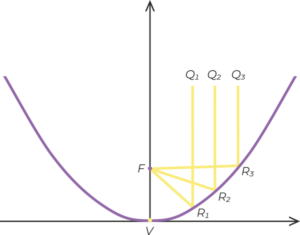
Ein Parabolreflektor ist eine gekrümmte Fläche mit der Querschnittsform einer Parabel. Er wird zur Ausrichtung von Licht- oder Schallwellen genutzt.
Sämtliche Licht- oder Schallwellen, die parallel zur Parabelachse in einen Parabolspiegel einfallen und auf die Innenfläche des Parabolspiegels auftreffen, werden in den Brennpunkt reflektiert.
Antennen von Radioteleskopen und Satellitenschüsseln nutzen dieses Konzept der Anbringung des Empfängers im Brennpunkt, um ein konzentriertes Signal zu erhalten.
Auf ähnliche Weise konzentriert der Parabolreflektor in einer Lampe das von der im Brennpunkt befindlichen Glühbirne ausgestrahlte Licht in einen gerichteten Lichtstrahl.
Dasselbe Prinzip findet bei den Scheinwerfern eures Autos und bei Reflektoren Anwendung.
Dort, wo von der Parabolantenne Schallwellen empfangen werden, richtet der parabolische Reflektor in einer Lampe die Lichtwellen nach draußen.
Weitere Anwendungen von parabolischen Kurven:
Ein gut bekanntes Beispiel einer Parabel in der Physik ist die Bahn eines Teilchens oder Körpers in Bewegung unter dem Einfluss der Schwerkraft (ohne Luftwiderstand).
Eine solche Bahn ist stets die Approximation einer Parabel und wurde Anfang des 17. Jahrhunderts von Galilei entdeckt.
Hängebrücke: die Parabel stellt das Profil des Seils der Hängebrücke dar.
Bogenbrücke: die Parabel stellt das Profil der Tragekonstruktion der Bogenbrücke dar.
Diese Betonbrücke überträgt ihr Gewicht waagerecht auf die Stützpfeiler.





