The Brachistochron Problem
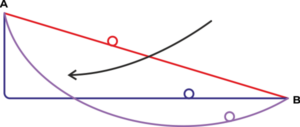
In 1696, Johann Bernoulli called for a problem in which a body located at a point should be triggered along a certain trajectory to a point below in the shortest time. Both points do not lie on a vertical line. We have to find the shape of this trajectory, which is called BRACHISTOCHRONA. Brachistos means the shortest, chronos means time. Several well-known physicists – Newton, Leibniz and Jakob Bernoulli – submitted the solution at the same time. It turned out that the sought curve is a so-called cycloid. The solution of this problem contributed to the development of a new field of mathematics – calculus of variations.
Check the property of the brachistochrona!
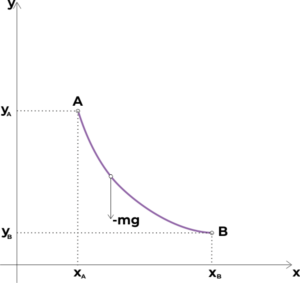
BRACHISTOCHONA is a curve connecting two points, after which the point of mass gets from the initial rest at one point to another by the action of a homogeneous gravitational field in the SHORTEST TIME.
What is a cycloid?
A cycloid is a curve that describes a point on the circumference of a wheel when the wheel is rolling on a plane.
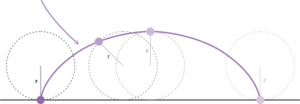
Galileo Galilei was fascinated by the cycloid and wrote the first work about it in 1599, where he also named it.
The length of one arc is 8r (does not depend on Pi)
The surface under one arc is equal to three times the surface of a rolled circle, ie 3π r2.
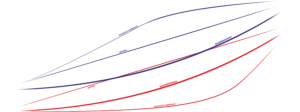
Concave trajectories
Straight line
Brachistochrona
Convex trajectories