Aufgabe zur Brachistochrone
1696 forderte Johann Bernoulli zur Lösung einer Aufgabe auf, bei der ein Körper, der sich an einem beliebigen Punkt befindet, innerhalb kürzester Zeit auf einer bestimmten Bahn an einen tiefer gelegenen Punkt bewegt werden soll. Dabei liegen die beiden Punkte nicht auf einer senkrechten Geraden. Wir sollen die Form dieser Bahn finden, die BRACHISTOCHRONE genannt wird. Brachistos bedeutet kürzeste, chronos bedeutet Zeit. Die Lösung der Aufgabe sandten mehrere bedeutende Physiker – Newton, Leibniz oder Jakob Bernoulli – gleichzeitig ein. Dabei zeigte sich, dass die gesuchte Kurve eine sog. Zykloide ist. Die Lösung dieser Aufgabe trug zur Entwicklung eines neuen Teilgebiets der Mathematik – der Variationsrechnung – bei.
Überprüfe die Eigenschaft der Brachistochrone!
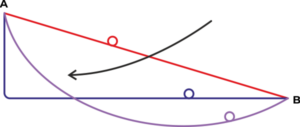
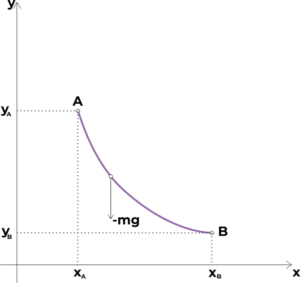
Eine BRACHISTOCHRONE ist eine zwei Punkte miteinander verbindende Kurve, auf der ein Massepunkt aus dem anfänglichen Ruhezustand in einem Punkt durch die Wirkung des homogenen Gravitationsfelds innerhalb KÜRZESTER ZEIT an den zweiten Punkt gelangt.
Was ist eine Zykloide?
Eine Zykloide ist die Kurve, die ein auf dem Umfang eines Rads befindlicher Punkt beschreibt, wenn das Rad auf einer Ebene gerollt wird.
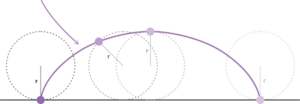
Galileo Galilei war von der Zykloide fasziniert. Er schrieb 1599 seine erste Schrift über sie, wo er sie auch benannte.
Die Länge eines Bogens ist 8r (unabhängig von Pi).
Die Fläche unter einem Bogen ist gleich dem Dreifachen der Fläche des gerollten Kreises, also 3π r2.
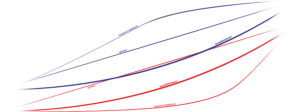
Konkave Bahnkurve
Gerade
Brachistochrone
Konvexe Bahnkurve