Gdybyś był przedsiębiorcą z Liberca, który postanowił odwiedzić klientów w dziewięciu różnych miastach, potem wrócić do Liberca i jednocześnie pokonać jak najmniej kilometrów, jak byś postąpił?
Problem podróżującego przedsiębiorcy to jedno z najbardziej znanych zadań optymalizacyjnych, ponieważ jego rozwiązanie wykorzystywane jest w praktyce w wielu zawodach, np. przez kuriera rozwożącego paczki, który chce jak najszybciej dotrzeć pod wszystkie adresy.
Często sam rozwiązujesz podobny problem, na przykład kiedy wchodzisz do galerii handlowej i wiesz, które sklepy chcesz odwiedzić. Szukasz takiej trasy, podczas której odwiedzisz wszystkie i jak najmniej się zmęczysz. Na końcu musisz wrócić do głównego wejścia.
W problemie podróżującego przedsiębiorcy zadanie polega na dotarciu z punktu A przez punkty B, C i D z powrotem do punktu A. Jednak najkrótszą możliwą drogą.
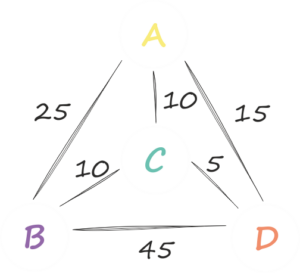
Odcinkowi pomiędzy dwoma punktami (miejscowościami) przyporządkowujesz wartość (odległość w km). Następnie wystarczy poszukać najmniejszej sumy wartości odcinków (tras), które trzeba pokonać, aby wykonać zadanie.
Jak postępować?
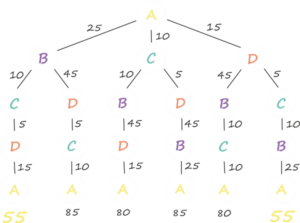
Zrobilibyśmy to za pomocą metody drzewa decyzyjnego. Za jego pomocą rysujemy absolutnie każdą możliwą trasę, którą możemy wybrać i która spełnia warunki (każde miejsce odwiedzimy tylko raz i trasę zakończymy tam, gdzie ją zaczęliśmy).
Jak by wyglądało to zadanie na mapie Czech?
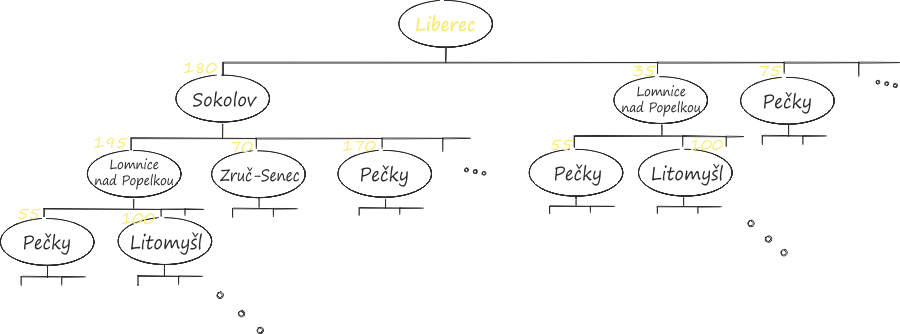
Jak widać, drzewo decyzyjne i liczba możliwych tras rośnie bardzo szybko wraz ze wzrostem liczby węzłów. Zbudowanie takiego drzewa już dla 10 miejsc zajęłoby człowiekowi bardzo wiele czasu. Dlatego pomagają nam w tym komputery, które obliczają długość wszystkich możliwych tras i znajdują najkrótszą z nich.
Całe drzewo decyzyjne nie zmieści się na naszej ścianie, ale zastanów się, ile możliwych tras ma nasz przedsiębiorca?
Ile minimalnie rozwiązań (najkrótszych tras) będzie zawsze poprawnych?





