If you were a businessman from Liberec who decides to visit customers in nine different cities, return to Liberec and drive as few kilometres as possible. How would you proceed?
The business salesman’s problem is one of the most well-known optimization tasks, as it is used in practice by many professions, such as a parcel courier, who wants to go through all the addresses as soon as possible.
You often solve a similar problem, for example when you walk into a shopping mall and know which stores you want to visit. You are looking for a way to visit everyone and do not be tired so much. At the end you have to go back to the main entrance. In the case of a business salesman’s problem, the task is to get from point A through points B, C and D back to point A. However, the by the shortest possible route.
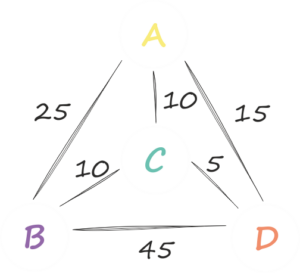
You assign a value (distance in km) to the line between every two points (municipalities). Then you are just looking for the smallest sum of line values that you have to go through to complete the task.
How to do it? We would go for it with the decision tree method. We use it to draw every path we can choose and it meets the conditions (we visit each place just once and end the path where we started it).
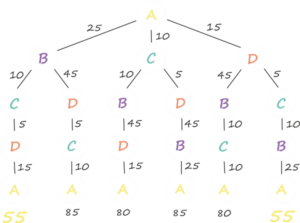
What would it look like for the task on the map of the Czech Republic?
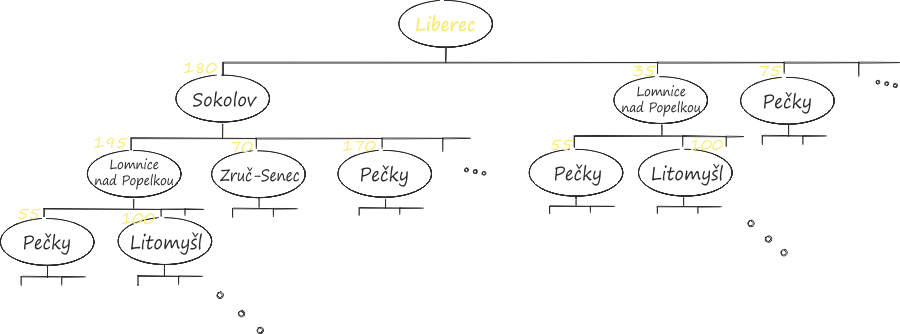
As you can see, the decision tree and the number of possible paths grow very sharply as the number of nodes increases. Creating such a tree for 10 places would take a very long time. Therefore, computers that calculate the length of all possible paths and find the shortest help us in this.
The whole decision tree doesn’t fit on our wall, but consider how many possible paths there are for our salesman?
At least how many correct solutions will always be (the shortest ways)?





