Wenn du ein Geschäftsmann aus Liberec wärst, der seine Kunden in neun verschiedenen Städten besuchen, dann nach Liberec zurückkehren und dabei so wenige Kilometer wie möglich fahren will, wie würdest du vorgehen?
Das Problem des Geschäftsreisenden ist eine der bekanntesten Optimierungsaufgaben, da sie in der Praxis viele Berufe nutzen, wie beispielsweise ein Paketkurier, der alle Adressen schnellstmöglich abfahren will.
Ein ähnliches Problem löst auch du häufig, zum Beispiel wenn du in ein Einkaufszentrum gehst und weißt, welche Geschäfte du besuchen willst. Du suchst einen solchen Weg, bei dem du alle besuchst und dabei am wenigsten ins Schwitzen gerätst. Am Ende musst du zum Haupteingang zurückkehren.
Beim Problem des Geschäftsreisenden ist deine Aufgabe, von Punkt A über die Punkte B, C und D zurück zu Punkt A zu kommen, allerdings auf der kürzesten Strecke.
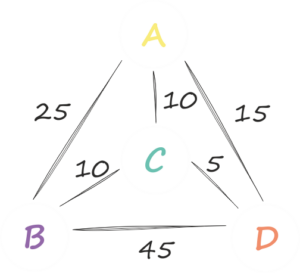
Jeder Strecke zwischen jeweils zwei Punkten (Gemeinden) ordnest du einen Wert (die Entfernung in km) zu. Danach suchst du die kleinste Summe der Werte der Strecken (Wege), die du abfahren musst, um deine Aufgabe zu erfüllen.
Wie geht man vor?
Wir würden dies mit der Methode eines Entscheidungsbaums angehen. Mit dessen Hilfe zeichnen wir wirklich jeden Weg, den wir wählen können und der die Bedingungen erfüllt (wir besuchen jeden Ort genau einmal und beenden den Weg dort, wo wir begonnen haben).
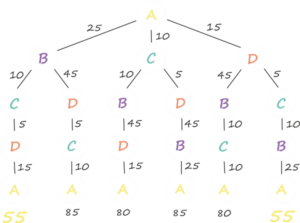
Wie würde das für die Aufgabe auf der Karte der Tschechischen Republik aussehen?
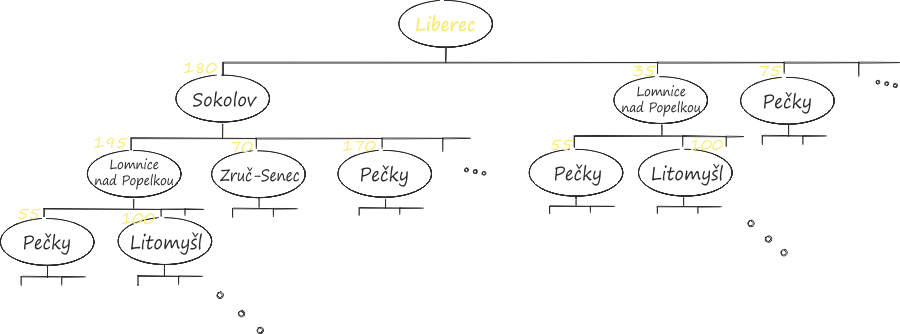
Wie zu sehen ist, wächst der Entscheidungsbaum und die Zahl der möglichen Wege bei Zunahme der Zahl der Knotenpunkte sehr steil. Die Erstellung eines solchen Baumes schon für 10 Orte durch einen Menschen würde sehr lange dauern. Deshalb helfen uns dabei Computer, die die Länge aller möglichen Wege berechnen und den kürzesten finden.
Der ganze Entscheidungsbaum passt nicht an unsere Wand, aber überlege, wie viele mögliche Wege es für unseren Geschäftsreisenden gibt?
Zumindest wie viele richtige Lösungen (kürzeste Wege) es immer gibt?





