Determining body volumes is one of the most common and oldest uses of geometry in practice.
Using the volume of bodies, we can, for example, determine the storage capacity of various spaces or containers, the weight of objects and many other data.
CAVALIER’S PRINCIPLE:
If the sections of two three-dimensional bodies with horizontal planes have the same content, then both bodies have the same volume.
Use of Cavalieri’s principle in calculating the volume of some bodies:

Volume of a prism or cylinder = volume of a block with the same base and height = content of bases x height

pyramids P2 and P1 have a common base A and a common height k
pyramids P1 and P3 also share base B and height h
volume P1, P2, P2 = 1/3 volume of prism = 1/3 x content of base x height = 1/3 x B x h
![]()
hemisphere volume = cylinder volume – cone volume = πr3 – 1/3 πr3 = 2/3 πr3
sphere volume = 2 x hemisphere volume = 4/3 πr3
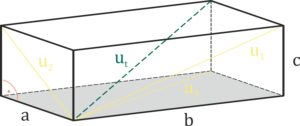
Block
a, b, c – sides of the body
u1, u2, u3 – wall diagonals
ut – body diagonal

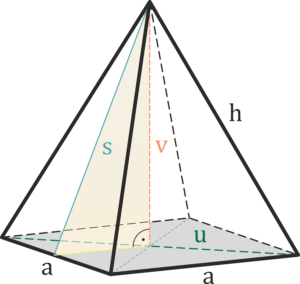
Pyramid
and – the side of the base of the body
h – side length
v – height of the body
u – diagonal of the base of the body
s – height of the body side
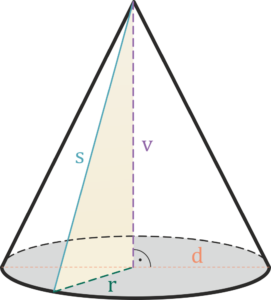
Cone
s – side of the casing
v – height of the body
r – radius of the circular base of the body
d – diameter of the circular base of the body

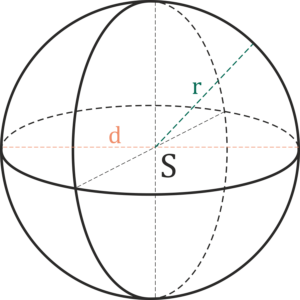
Ball
r – radius of the sphere
d – diameter of the sphere
S – center of the sphere