Die Bestimmung der Volumen von Körpern ist eine der häufigsten und ältesten Anwendungsarten der Geometrie in der Praxis.
Mit Hilfe des Volumens von Körpern kann man z. B. die Lagerkapazität verschiedener Räume oder Gefäße, die Masse von Gegenständen und viele weitere Angaben ermitteln.
PRINZIP VON CAVALIERI:
Wenn die Schnittflächen zweier dreidimensionaler Körper in den waagerechten Ebenen den gleichen Flächeninhalt haben, dann haben beide Körper dasselbe Volumen.
Anwendung des Cavalierischen Prinzips bei der Berechnung des Volumens einiger Körper:

Volumen eines Prismas oder Zylinders = Volumen eines Quaders mit derselben Grundfläche und Höhe = Flächeninhalt der Grundfläche x Höhe

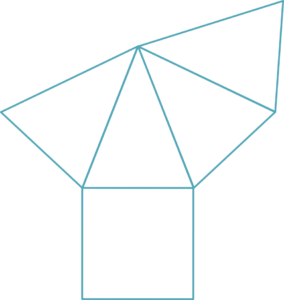
Die Pyramiden P2 und P1 haben die gemeinsame Grundfläche A und die gemeinsame Höhe k.
Die Pyramiden P1 und P3 teilen ebenfalls die Grundfläche B und die Höhe h.
Volumen P1, P2, P3 = 1/3 des Volumens des Prismas = 1/3 x Flächeninhalt der Grundfläche x Höhe = 1/3 x B x h

Volumen der Halbkugel = Volumen des Zylinders – Volumen des Kegels = πr3 – 1/3 πr3 = 2/3 πr3
Volumen der Kugel = 2 x Volumen der Halbkugel = 4/3 πr3
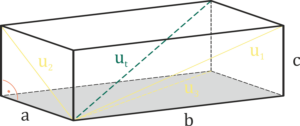
Quader
a, b, c – Seiten des Körpers
u1, u2, u3 – Seitendiagonalen
ut – Raumdiagonale

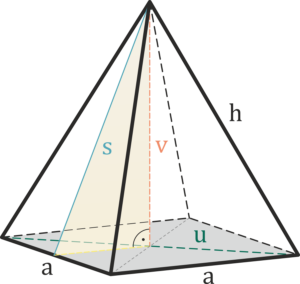
Pyramide
a – Seite der Grundfläche des Körpers
h – Länge der Seite
v – Höhe des Körpers
u – Diagonale der Grundfläche des Körpers
s – Höhe der Körperseite
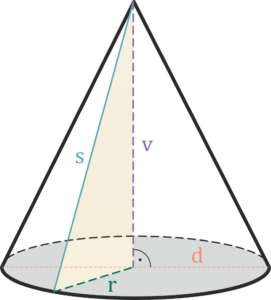
Kegel
s – Seite des Mantels
v – Höhe des Körpers
r – Radius der Kreisgrundfläche des Körpers
d – Durchmesser der Kreisgrundfläche des Körpers

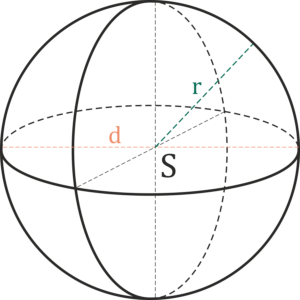
Kugel
r – Radius der Kugel
d – Durchmesser der Kugel
S – Mittelpunkt der Kugel