Gra cieni jest starym sposobem opowiadania historii i formą rozrywki, wykorzystującą płaskie figury (lalki cieniowe) trzymane między źródłem światła a półprzezroczystym ekranem lub płótnem.
Teatr cieni ma długą historię i jest popularny w różnych kulturach południowo-wschodniej Azji, Chin i Europy. Zasada gry cieni w miarę rozwoju fotografii została wykorzystana w wyświetlaniu diapozytywów, a w końcu w kinematografii. Wspólną zasadą tych mediów jest kreatywne wykorzystanie światła i powierzchni projekcyjnej w połączeniu z tworzeniem obrazu na bazie przezroczystości.
Zasadę gry cieni możesz sprawdzić na naszej pomocy dydaktycznej. Obserwuj, w jakiej odległości od siebie musisz umieścić przedmioty o tym samym kształcie i różnej wielkości, aby ich cień był tej samej wielkości. Możesz również połączyć kilka kształtów w różnych odległościach, aby stworzyć złożoną panoramę.
Obserwacja cieni w przyrodzie może nam dostarczyć ciekawych informacji. Na przykład grecki uczony Arystoteles doświadczalnie wydedukował kulisty kształt Ziemi z obserwacji cienia Ziemi podczas zaćmienia Księżyca. Zasada podobna do gry cieni – oparta na funkcji liniowej – umożliwia leśnikom mierzenie wysokości drzew lub geodetom określanie wysokości budynków tylko za pomocą pomiaru kątów z precyzyjnych obserwacji optycznych. Więcej informacji na temat tego zastosowania można otrzymać z eksponatu Twierdzenie Talesa.
Funkcja liniowa to funkcja, której wartość zmienia się proporcjonalnie niezależnie od zmiennej.
Funkcja liniowa na zbiorze liczb rzeczywistych to każda funkcja f, określona wzorem:
ƒ : y = ax + b
gdzie a, b∈R. Dziedziną funkcji jest zbiór wszystkich liczb rzeczywistych Dy = R.
Wykresem funkcji kwadratowej jest prosta. Ważnymi punktami wykresu funkcji linowej są punkty przecięcia prostej z osiami współrzędnych x i y.
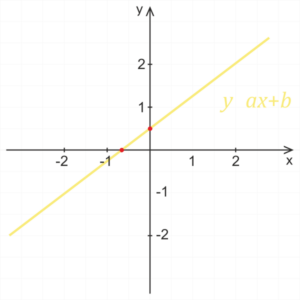
Wpływ współczynników a,b na wykres funkcji liniowej.
Wpływ współczynnika a
Dla dodatniego współczynnika funkcja liniowa jest rosnąca, dla ujemnego współczynnika a funkcja jest malejąca. Im większa jest wartość absolutna współczynnika a, tym bardziej wykres funkcji jest zbliżony do osi y. Jeżeli wartość absolutna współczynnika a jest mniejsza niż jeden, to wraz z malejącą wartością absolutną współczynnika a wykres funkcji bardziej zbliża się do osi x.
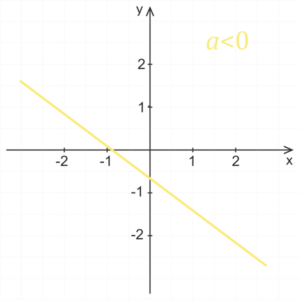
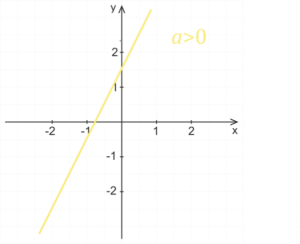
Wpływ współczynnika b
Wykres funkcji przecina oś y w punkcie z igrekową współrzędną równą współczynnikowi b.
a = 0
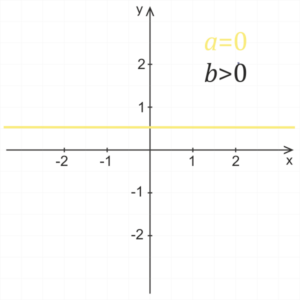
Dla zerowego współczynnika uzyskujemy równanie , co jest zapisem funkcji stałej.
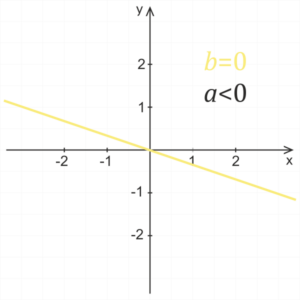
b = 0
Dla zerowego współczynnika b uzyskujemy równanie , co jest zapisem funkcji liniowej, której wykres przechodzi przez początek układu współrzędnych.
Obliczenie punktu przecięcia wykresu funkcji liniowej y = ax + b z osią x
Każdy punkt leżący na osi ma igrekową współrzędną równą zeru, po podstawieniu w zapisie funkcji liniowej otrzymamy równanie liniowe, którego rozwiązanie wskaże punkt przecięcia:
ax+b=0 x=-b/a;a≠0
Obliczenie punktu przecięcia wykresu funkcji liniowej y = ax + b z osią y
Każdy punkt leżący na osi ma iksową współrzędną równą zeru, po podstawieniu w zapisie funkcji liniowej otrzymamy igrekową współrzędną danego punktu przecięcia:
y=0x+by= b





