Ein Schattenspiel ist eine althergebrachte Form des Erzählens und der Unterhaltung, die flache Figuren (Schattenpuppen) nutzt, die zwischen eine Lichtquelle und einen lichtdurchlässigen Bildschirm oder einer Leinwand gehalten werden.
Das Schattentheater hat eine lange Geschichte und ist in verschiedenen Kulturen Südostasiens, Chinas und Europas beliebt. Das Prinzip des Schattenspiels entwickelte sich mit der Entwicklung der Fotografie zur Diaprojektion und schließlich zur Kinematographie. Das gemeinsame Prinzip dieser Medien ist die kreative Nutzung von Licht und einer Projektionsfläche in Verbindung mit der Schaffung eines Bildes anhand von Lichtdurchlässigkeit.
An unserem didaktischen Hilfsmittel kannst du das Prinzip des Schattenspiels ausprobieren. Beobachte, in welcher Entfernung Gegenstände derselben Form und unterschiedlicher Größe angebracht werden müssen, damit ihr Schatten gleich groß ist. Du kannst auch mehrere Formen und verschiedene Entfernungen kombinieren und so ein kompliziertes Panorama schaffen.
Die Beobachtung von Schatten in der Natur kann uns interessante Informationen bringen. Der griechische Gelehrte Aristoteles beispielsweise leitete die Kugelform der Erde experimentell von der Beobachtung des Schattens der Erde bei einer Mondfinsternis ab. Ein ähnliches Prinzip wie beim Schattenspiel – das auf einer linearen Funktion basiert – ermöglicht es den Waldarbeitern, die Höhe von Bäumen zu messen, oder den Geodäten, die Höhe von Gebäuden zu bestimmen, und dies nur mittels Messung von Winkeln aus genauen optischen Beobachtungen. Mehr zu dieser Applikation erfahrt ihr beim Hilfsmittel Satz des Thales.
Eine lineare Funktion ist eine Funktion, deren Funktionswert sich proportional zur unabhängigen Variablen ändert.
Eine lineare Funktion in der Menge der reellen Zahlen ist jede Funktion f, die durch folgende Vorschrift gegeben ist:
ƒ : y = ax + b
wobei a, b∈R. Definitionsbereich sind alle reellen Zahlen Dy = R.
Der Graph einer linearen Funktion ist eine Gerade. Wichtige Punkte des Graphen einer linearen Funktion sind die Schnittpunkte der Geraden mit den Koordinatenachsen x und y.
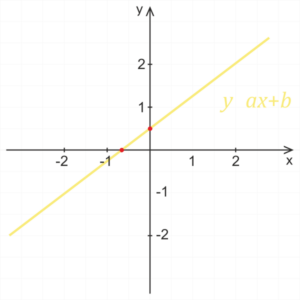
Einfluss der Koeffizienten a,b auf den Graphen der linearen Funktion.
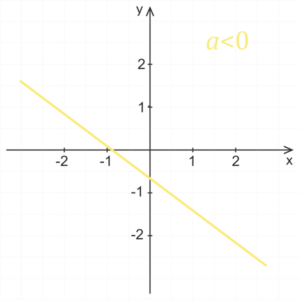
Einfluss des Koeffizienten a
Für einen positiven Koeffizienten a ist die lineare Funktion steigend, für einen negativen Koeffizienten a ist die Funktion fallend. Je größer der absolute Wert des Koeffizienten a, umso mehr schmiegt sich der Graph der Funktion an die y-Achse an. Ist der absolute Wert des Koeffizienten a kleiner Eins, dann schmiegt sich der Graph der Funktion mit sinkendem absolutem Wert des Koeffizienten a immer mehr an die x-Achse an.
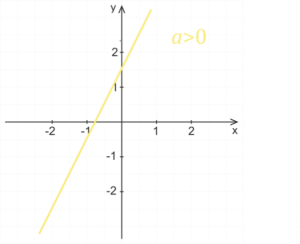
Einfluss des Koeffizienten b
Der Graph der Funktion schneidet die y-Achse in dem Punkt mit der y-Koordinate gleich dem Koeffizienten b.
a = 0
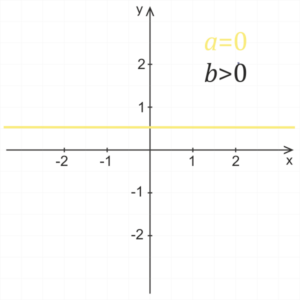
Für den Null-Koeffizienten a erhalten wir die Vorschrift y = b, was die Vorschrift einer konstanten Funktion ist.
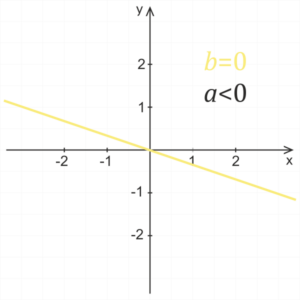
b = 0
Für den Null-Koeffizienten b erhalten wir die Vorschrift y = ax, was die Vorschrift einer linearen Funktion ist, deren Graph durch den Ursprung des Koordinatensystems verläuft.
Berechnung des Schnittpunkts des Graphen der linearen Funktion y = ax + b mit der x-Achse
Die y-Koordinate jedes Punktes, der auf der x-Achse liegt, ist gleich Null, nach dem Einsetzen von y = 0 erhalten wir in der Vorschrift der linearen Funktion eine lineare Gleichung, durch deren Lösung wir den geforderten Schnittpunkt erhalten:
ax+b=0 x=-b/a;a≠0
Berechnung des Schnittpunkts des Graphen der linearen Funktion y = ax + b mit der y-Achse
Die x-Koordinate jedes Punktes, der auf der y-Achse liegt, ist gleich Null, nach dem Einsetzen von x = 0 erhalten wir in der Vorschrift der linearen Funktion die y-Koordinate des geforderten Schnittpunkts:
y=0x+by= b





