Pochodna funkcji jest ważnym pojęciem w analizie matematycznej i podstawą rachunku różniczkowego. Została opisana w XVII wieku dzięki odkryciom Newtona i Leibniza w rozwiązywaniu problemów geometrycznych i fizycznych. Odgrywa ważną rolę w określaniu przebiegu funkcji, ponieważ pochodna funkcji opisuje zmianę wartości funkcji względem zmian zmiennej niezależnej. W przypadku dwuwymiarowego wykresu funkcji f(x) pochodna tej funkcji jest w dowolnym punkcie równa współczynnikowi kierunkowemu stycznej do tego wykresu. Styczna tworzy z osią x kąt, a tangens tego kąta nazywamy współczynnikiem kierunkowym funkcji. Pochodna funkcji w punkcie może być przybliżona z wystarczającą dokładnością właśnie jako współczynnik kierunkowy stycznej. Jeśli krzywa w punkcie x jest rosnąca, to jej pochodna będzie >0, a jeśli jest malejąca, to pochodna będzie <0.
Jeżeli w danym punkcie istnieje pochodna, to jest ona jedyna. Żadna funkcja nie ma więcej niż jednej pochodnej w jednym punkcie. Jeżeli funkcja ma pochodną w danym punkcie, to funkcja jest w tym punkcie ciągła. Jeśli jednak funkcja jest ciągła w danym punkcie, nie oznacza to, że ma tam pochodną. Typowym przykładem jest funkcja f(x) = |x|. Wykres jest szpiczasty i nie można obliczyć kierunkowej stycznej w tym wierzchołku.
Czasami potrzebujemy znać wartość tzw. drugiej pochodnej. Jej obliczenie nie jest to skomplikowane, po prostu raz wyznaczamy pochodną funkcji, a następnie wyznaczamy wynik po raz drugi. Oznaczamy to dwoma kreskami: f“(x) = (f'(x))‘.
- Pochodna – współczynnik kierunkowy stycznej
- Pochodna nie istnieje
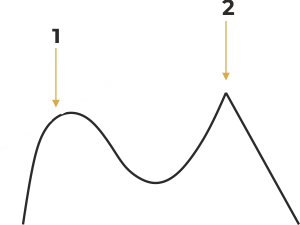
Minimum i maksimum funkcji
Znalezienie punktów, w którym wartość funkcji osiąga minimum lub maksimum – tzw. ekstremum funkcji, jest ważne dla zrozumienia przebiegu funkcji oraz dla rozwiązywania skomplikowanych zadań, takich jak np. regresja nieliniowa (optymalizacja procesów). Ekstrema można łatwo znaleźć za pomocą pochodnej funkcji, ponieważ w tych punktach pochodna musi być zerowa. Zadanie to jest bardzo podobne do sytuacji człowieka idącego w mgle na wzgórze – jak sprawdzimy, że znajdujemy się na jego szczycie?
Od wystrzału z działa po kosmos
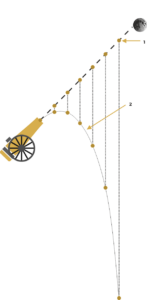
Tor ciała poruszającego się w polu grawitacyjnym można aproksymować krzywymi stożkowymi. Satelity obiegające Ziemię poruszają się po kole, natomiast niektóre komety w układzie słonecznym poruszają się po torze bardzo zbliżonym do paraboli. Prędkość niezbędna do pokonania siły grawitacji ciała niebieskiego nazywana jest prędkością kosmiczną
Pierwsza prędkość kosmiczna oznacza prędkość po zamkniętej orbicie w polu grawitacyjnym Ziemi:
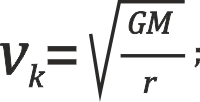
gdzie vk to prędkość, G stała grawitacji, M masa ciała niebieskiego, a r promień ciała niebieskiego.
Druga prędkość kosmiczna, inaczej prędkość ucieczki, to minimalna prędkość, z jaką musi się poruszać ciało w polu grawitacyjnym innego ciała, by móc opuścić to pole grawitacyjne. Obiegające ciało porusza się z tą prędkością po trajektorii parabolicznej:
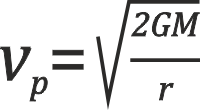
Trzecia prędkość kosmiczna to prędkość ucieczki potrzebna do opuszczenia pola grawitacyjnego Słońca. Dla jej obliczenia stosujemy wzór na drugą prędkość kosmiczną, gdy w miejsce masy wstawiamy masę Słońca. Obiegające ciało porusza się z tą prędkością po trajektorii hiperbolicznej.
Satelity obiegające Ziemię poruszają się po kole, natomiast niektóre komety w układzie słonecznym poruszają się po torze bardzo zbliżonym do elipsy lub paraboli.
Jeśli uwzględni się wpływ oporu powietrza, ciała (kula armatnia, rzucony kamień) poruszają się po tzw. krzywej balistycznej.
Krzywa balistyczna to krzywa, po której poruszałoby się ciało wyrzucone lub wystrzelone blisko powierzchni Ziemi, zazwyczaj w kierunku skośnym do góry. Oprócz przyspieszenia grawitacyjnego oddziałują na niego także siły aerodynamiczne. Na torze lotu ciała są trzy istotne punkty – punkt wylotu, wierzchołek toru i punkt upadku.