Derivation is an important concept in mathematical analysis and the basis of differential calculus. It was created in the 17th century thanks to the discoveries of Newton and Leibniz in solving geometric and physical problems. It plays an important role in determining the course of a function, because the derivative describes the change in the value of the function in relation to the change in the independent variable. In the case of a two-dimensional graph of the function f (x), the derivative of this function at any point is equal to the direction of the tangent of its graph. The tangent makes an angle with the x-axis, and the tangent of this angle is called the tangent direction. The derivative of a function at a point can be approximated with sufficient accuracy just like this tangent directive. If the curve is ascending at point x, its derivative will be> 0 and if it is decreasing, its derivative will be <0.
If there is a derivative at the point, it is the only one. No function has multiple derivatives at one point. If a function at a point has a derivative, then the function at that point is continuous. However, if a function is continuous at a given point, it does not mean that it is derivable here. A typical example is the function f (x) = | x |. The graph is at peak, and the tangent direction of the tangent at this peak cannot be calculated.
Sometimes we need to know the so-called the second derivative. This is not complicated, we simply derive the function once, and then derive the result a second time. We denote this by two commas: f “ (x) = (f ‚(x))‘.
- Derivation – tangent directive
- Derivation does not exist

The satellites orbiting the Earth move in circles, the orbits of some comets in the solar system are very close to ellipses or parabolas.
Minimum and maximum of function
Finding points where the functional value reaches either maxima or minima – the so-called extremes of the function – is important for understanding the shape of the function and also for solving complex tasks such as nonlinear regression (process optimization). The extremes can be found easily by deriving the function, because the derivative must be zero at these points. This task is very similar to a man climbing a hill in a fog – how do you know that you reached the top?
From cannon shot to space
The trajectory of a body moving in a gravitational field can be approximated by conic sections. The satellites orbiting the Earth move in a circle, the orbits of some comets in the solar system are very close to the parabolas. The speed required to overcome the gravitational force of a cosmic body is called the escape (or cosmic) velocity.
1st Cosmic velocity denotes the circular velocity in the Earth’s gravitational field:
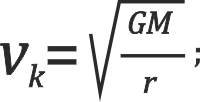
where vk is the velocity, G is the gravitational constant, M is the mass of the orbiting body, and r is the distance between the centers of the two bodies.
2nd Cosmic (Escape) velocity is the minimum velocity at which a body must move in another body’s gravitational field in order to leave that gravitational field. The orbiting body moves along a parabolic trajectory:

3rd Cosmic (Escape) velocity is the escape velocity from the gravitational field of the Sun. For determining its value, the relationship for the 2nd escape velocity applies, into which we substitute the mass of the Sun for the mass M. The body moves along a hyperbolic trajectory.
When the effect of air resistance is taken into account, the bodies (such as cannonball, thrown stone) move along the so-called ballistic curve.
A ballistic curve is a space curve described by a body thrown or fired near the earth’s surface, usually obliquely upwards. In addition to gravitational acceleration, aerodynamic forces also act on it. There are three significant points on the body’s flight path – the point of the shot, the top of the path and the point of reach.






