Die Ableitung ist ein wichtiger Begriff der mathematischen Analysis und die Grundlage der Differentialrechnung. Sie entstand im 17. Jahrhundert dank den Entdeckungen von Newton und Leibniz bei der Lösung geometrischer und physikalischer Probleme. Sie hat eine bedeutende Rolle bei der Bestimmung des Funktionsverlaufs, denn die Ableitung beschreibt die Änderung des Funktionswerts im Verhältnis zur Änderung der unabhängigen Variablen. Beim zweidimensionalen Graphen der Funktion f(x) ist die Ableitung dieser Funktion in einem beliebigen Punkt gleich der Steigung der Tangente dieses Graphen. Die Tangente schließt einen Winkel mit der x-Achse ein und den Tangens dieses Winkels nennt man Steigung der Tangente. Die Ableitung einer Funktion in einem Punkt kann mit ausreichender Genauigkeit gerade als diese Tangentensteigung approximiert werden. Ist die Kurve im Punkt x zunehmend, ist ihre Ableitung > 0, ist sie abnehmend, ist die Ableitung < 0.
Gibt es in einem Punkt eine Ableitung, dann ist sie die einzige. Keine Funktion hat in einem Punkt mehrere Ableitungen. Hat eine Funktion in einem Punkt eine Ableitung, dann ist die Funktion in diesem Punkt stetig. Ist jedoch eine Funktion in einem gegebenen Punkt stetig, bedeutet das nicht, dass sie hier differenzierbar ist. Ein typisches Beispiel ist die Funktion f(x) = |x|. Der Graph läuft spitz zu, und in dieser Spitze kann die Tangentensteigung nicht berechnet werden.
Manchmal muss man die sog. zweite Ableitung kennen. Es handelt sich um nichts Kompliziertes, man leitet die Funktion einfach einmal ab und anschließend leitet man das Ergebnis noch ein zweites Mal ab. Dies wird durch zwei Striche gekennzeichnet: f“(x) = (f'(x))‘.
- Ableitung – Steigung der Tangente
- Ableitung gibt es nicht
Satelliten, die die Erde umkreisen, bewegen sich auf einer Kreisbahn. Die Bahnen, auf denen sich einige Kometen im Sonnensystem bewegen, sind Ellipsen oder Parabeln sehr ähnlich.
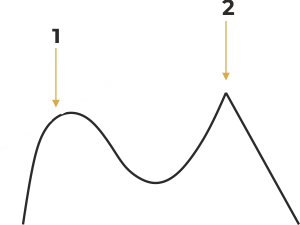
Minimum und Maximum der Funktion
Das Finden der Punkte, an denen der Funktionswert entweder sein Maximum oder sein Minimum erreicht, also der sog. Extremwerte der Funktion, ist wichtig für das Verständnis des Funktionsverlaufs sowie für die Lösung komplizierter Aufgaben, wie z. B. der nichtlinearen Regression (Prozessoptimierung). Die Extremwerte sind mit Hilfe der Funktionsableitung leicht zu finden, denn an diesen Punkten muss die Ableitung Null sein. Diese Aufgabe ähnelt sehr einem Menschen, der im Nebel auf einen Berg steigt – wie findet man heraus, dass man sich auf seinem Gipfel befindet?
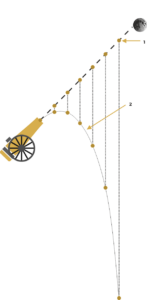
Vom Abschuss aus der Kanone bis ins Weltall
Die Bahn eines Körpers, der sich in einem Gravitationsfeld bewegt, kann mit Kegelschnitten approximiert werden. Satelliten, die die Erde umkreisen, bewegen sich auf einer Kreisbahn. Die Bahnen, auf denen sich einige Kometen im Sonnensystem bewegen, sind Parabeln sehr ähnlich. Die zum Überwinden der Gravitationswirkung eines kosmischen Körpers erforderliche Geschwindigkeit heißt kosmische Geschwindigkeit.
Die 1. kosmische Geschwindigkeit kennzeichnet die Kreisbahngeschwindigkeit im Gravitationsfeld der Erde:
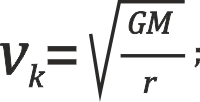
wobei vk die Geschwindigkeit, G die Gravitationskonstante, M die Masse des umkreisten Körpers und r der Abstand der Mittelpunkte beider Körper voneinander ist.
Die 2. kosmische Geschwindigkeit, auch Fluchtgeschwindigkeit, ist die Mindestgeschwindigkeit, mit der sich ein Körper im Gravitationsfeld eines anderen Körpers bewegen muss, um dieses Gravitationsfeld zu verlassen. Ein umkreisender Körper bewegt sich bei ihr auf einer Parabelbahn:
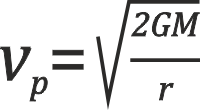
Die 3. kosmische Geschwindigkeit ist die Fluchtgeschwindigkeit aus dem Gravitationsfeld der Sonne. Für ihre Größe gilt also das Verhältnis für die 2. Fluchtgeschwindigkeit, in das als Masse die Masse der Sonne eingesetzt wird. Ein Körper bewegt sich bei ihr auf einer Hyperbelbahn.
Bei der Einberechnung des Einflusses des Luftwiderstands bewegen sich die Körper (Kanonenkugel, geworfener Stein) auf einer sog. ballistischen Kurve.
Die ballistische Kurve ist eine Raumkurve, die ein Körper beschreibt, der in der Nähe der Erdoberfläche gewöhnlich schräg nach oben geworfen oder abgeschossen wird. Neben der Erdschwerebeschleunigung wirken auch aerodynamische Kräfte auf ihn ein. Auf der Flugbahn des Körpers gibt es drei bedeutsame Punkte – den Abschusspunkt, den Gipfelpunkt und den Auftreffpunkt.