Jak można zmierzyć obiekt, jeśli nie sięgasz jego szczytu taśmą mierniczą?
Odpowiedź brzmi: Wykorzystując podobieństwo trójkątów prostokątnych. Ludzie wymyślili tę sztuczkę tysiące lat temu. Starogrecki matematyk Tales po raz pierwszy rozwiązał ten problem, gdy chciał poznać wysokość Wielkiej Piramidy.
Ciało i cień Talesa tworzą dwa boki wyobrażonego trójkąta prostego. W tym typie trójkąta jeden kąt ma 90°, a pozostałe dwa razem mają 90°.
Promienie słoneczne są mniej więcej równoległe, co oznacza, że światło pada na Talesa i piramidę pod tym samym kątem.
Bok piramidy jest skośny. Aby otrzymać wyobrażony trójkąt, musimy do długości cienia dodać długość połowy podstawy.
Jeśli dwa kąty w trójkącie są takie same, to dwa boki muszą też być takie same.
A więc… gdy promienie słońca padały pod kątem 45°, Tales wiedział, że jego cień ma taką samą długość jak jego wysokość.
A więc… cień piramidy plus połowa podstawy ma taką samą długość co wysokość piramidy.
A więc… jeżeli a = a, to b = b.
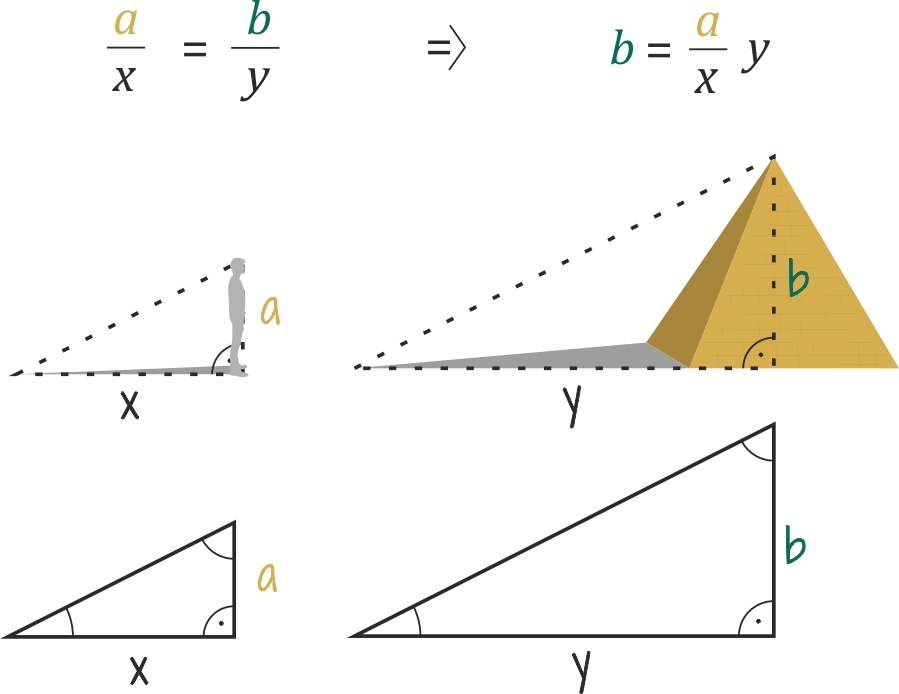
Matematycy rozwinęli później twierdzenie Talesa i uświadomili sobie, że obiekty można mierzyć, wykorzystując trójkąty w jakimkolwiek kącie nachylenia. Ponieważ oba cienie stworzyłyby podobne trójkąty – trójkąty, które mają takie same kąty i proporcje, chociaż mają inną wielkość.
A więc obowiązuje zasada: