How can you measure an object if you can’t reach its top by a line gauge?
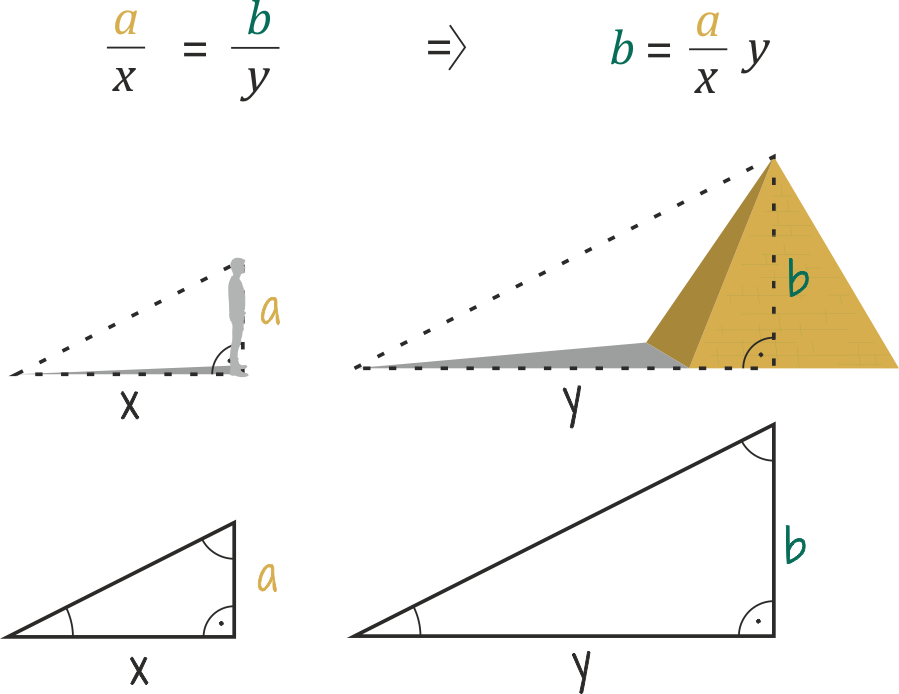
The answer is: Utilizing the similarity of right triangles. People came up with this trick already thousands of years ago. The problem was solved first by the ancient Greek mathematician Thales, when he wanted to know the height of the Great Pyramid.
Thales‘ body and shadow form two sides of an imaginary right triangle. In this type of triangle, one angle is 90 ° and the sum of other two is 90 °.
The sun rays are more or less parallel, which means that light falls on Thales and the pyramid at the same angle.
The side of the pyramid is sloping. To get an imaginary triangle, we must add half of the base to the length of the shadow.
If two angles in a triangle are the same, then the ratio of these two sides must be the same.
And so … when the sun rays fell at a 45 ° angle, Thales knew that his shadow was the same length as his height.
if you don’t reach the top?
And so … the shadow of the pyramid plus half the base is the same length as the height of the pyramid.
Finally … if a = a, then b = b
Later, mathematicians developed Thales‘ idea further and realized that objects can be measured using triangles at any angle. Because both shadows would form similar triangles – triangles that have the same angles and proportions, although they have a different size.
And so: