Wie kann man ein Objekt vermessen, wenn man mit dem Maßband nicht bis an seine Spitze reicht?
Die Antwort lautet: Mit Hilfe der Ähnlichkeit rechtwinkliger Dreiecke. Auf diesen Trick kamen die Menschen bereits vor Tausenden Jahren. Als Erster löste dieses Problem der altgriechische Mathematiker Thales, als er die Höhe der Großen Pyramide wissen wollte.
Thales Körper und sein Schatten bilden zwei Seiten eines gedachten rechtwinkligen Dreiecks. Bei dieser Art von Dreieck hat ein Winkel 90° und die anderen beiden zusammen 90°.
Die Sonnenstrahlen verlaufen mehr oder weniger parallel, was bedeutet, dass das Licht unter demselben Winkel auf Thales und die Pyramide einfällt.
Die Seite der Pyramide ist schräg. Wenn man ein gedachtes Dreieck erhalten will, muss man die Länge der Hälfte der Basis zur Länge des Schattens hinzurechnen.
Wenn zwei Winkel im Dreieck gleich sind, müssen auch zwei Seiten gleich sein.
Und demzufolge … Als die Sonnenstrahlen unter einem Winkel von 45° einfiele, wusste Thales, dass sein Schatten dieselbe Länge hat, wie er groß ist.
Und demzufolge … Der Schatten der Pyramide plus die Hälfte der Basis haben dieselbe Länge, wie die Höhe der Pyramide.
Und demzufolge … Wenn a = a, dann b = b
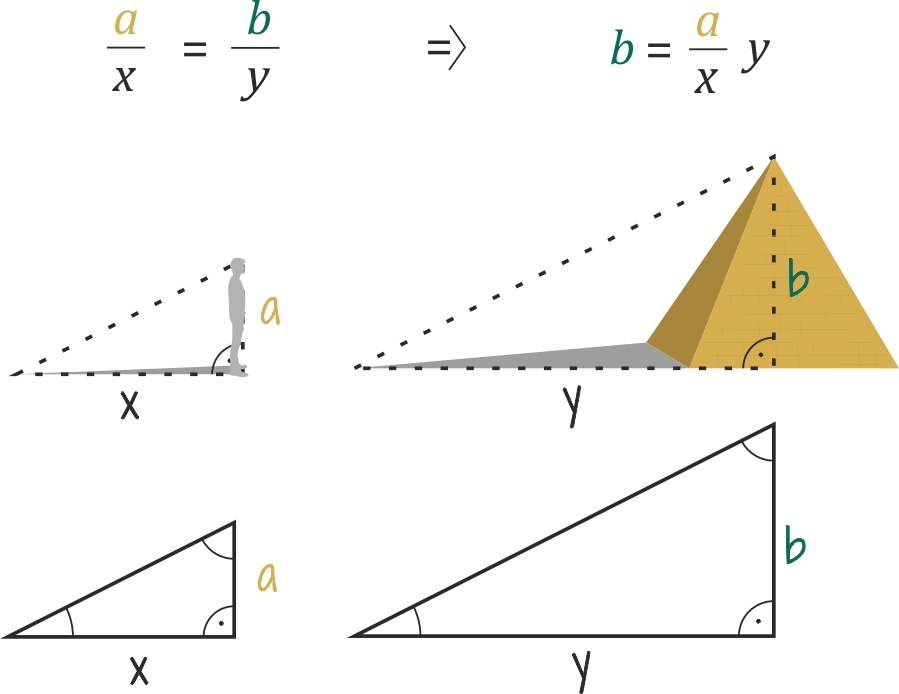
Später entwickelten Mathematiker Thales‘ Gedanken weiter und wurden sich bewusst, dass Objekte mit Hilfe von Dreiecken in jedem Neigungswinkel gemessen werden können. Weil beide Schatten ähnliche Dreiecke bilden würden – Dreiecke, die dieselben Winkel und Proportionen haben, auch wenn sie eine andere Größe haben.
Es gilt also: