LICZBY W PRZYRODZIE
Ciąg Fibonacciego
Liczby Fibonacciego tworzą chyba najsłynniejszy ciąg nazwany imieniem Fibonacciego, czyli Leonarda z Pizy. Każda liczba tego ciągu jest sumą dwóch poprzednich liczb, czyli na przykład
2 = 1 + 1 ; 3 = 1 + 2 ; 5 = 2 + 3 i tak dalej.

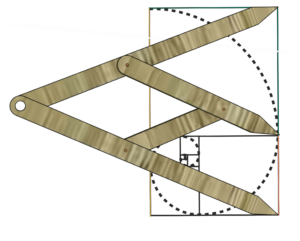
Jeżeli stopniowo skonstruujemy kwadraty o bokach, których długość jest równa liczbom Fibonacciego 1,1, 2, 3, 5, 8, 13, 21, 34…., to można je pięknie poukładać obok siebie. Jeżeli w każdym z nich narysujemy ćwiartkę okręgu, powstanie spirala Fibonacciego.
Liczby Fibonacciego znajdują się w strukturach spiralnych na powierzchni szyszek drzew iglastych i ananasa, na tarczy słonecznika, stokrotce i innych kwiatach. Na wskazanych roślinach można zaobserwować dwa układy spirali. Spirale lewoskrętne i prawoskrętne. Liczby spirali w obu kierunkach zawsze odpowiadają wielkości rośliny lub można je wyrazić sąsiednimi elementami ciągu Fibonacciego. Na przykład w słoneczniku najczęściej w jednym kierunku są 34 spirale, a w drugim kierunku 55 spirali.
Ciekawe jest obserwowanie liczby płatków kwiatów różnych roślin. Bardzo często występują kwiaty, w których liczba płatków jest jakąś liczba Fibonacciego. Przykłady: 1 płatek: kalia, anturium, 2 płatki: wilczomlecz, 3 płatki: kosaciec, 5 płatków: niezapominajka, 8 płatków: glistnik jaskółcze ziele, 13 płatków: jeżówka, 21 płatków: cykoria podróżnik, 34 płatki: jastrun.
Liczby Fibonacciego często występują również tam, gdzie jest złoty podział. Prostokąty, które widzimy w budowie kwadratowej spirali, są nie do odróżnienia od złotych prostokątów.
„Geometria ma dwa wielkie skarby: jednym z nich jest twierdzenie Pitagorasa, a drugim złoty podział.
Pierwszy z nich możemy porównać do złota, drugi do drogocennego klejnotu”.
Bez względu na formę przedstawienia złotego podziału zawsze ma on w sobie pewną prostotę i elegancję.
Johannes Kepler
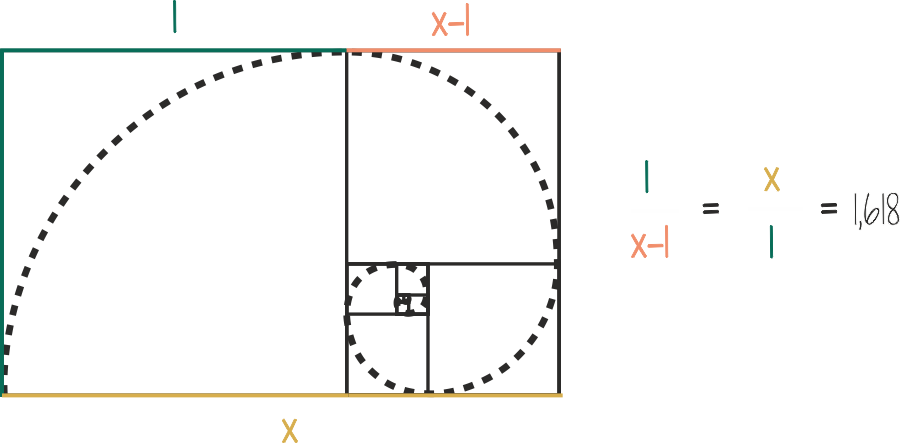
Matematycznie:
Jeżeli złoty podział to x, to
x2 – x – 1 = 0,
co można zapisać jako
x/1 = 1/(x-1).
Wyrażając słowami:
„Złoty podział to stosunek, w jakim całość do większej części ma się tak samo, jak większa część ma się do części mniejszej”.
Dobrym przykładem złotego podziału (złotej proporcji) jest karta kredytowa, której wielkość jest zestandaryzowana w skali ogólnoświatowej. Jest zgodna z definicją złotego podziału. Złoty prostokąt to kształt popularny ze względu na jego zrównoważony wygląd – nie jest ani zbyt długi, ani zbyt szeroki.
Jak sprawdzić, czy prostokąt jest złoty?
Połóż dwa prostokąty obok siebie: jeden pionowo, drugi obok poziomo. Jeżeli przedłużysz przekątną poziomo ułożonego prostokąta i przetnie ona górny wierzchołek drugiego prostokąta, to oba są złote.
Znajdź złoty podział na ciele człowieka.
Znajdź i sprawdź złoty podział: