ZAHLEN IN DER NATUR
Fibonacci-Folge
Die Fibonacci-Zahlen bilden die wohl berühmteste Folge, die nach Fibonacci, alias Leonardo da Pisa, benannt wurde. Jede Zahl in dieser Folge ist die Summer der zwei vorhergehenden Zahlen, also zum Beispiel
2 = 1 + 1 ; 3 = 1 + 2 ; 5 = 2 + 3 und so weiter.

Wenn man nach und nach Quadrate mit Seiten konstruiert, deren Längen den Fibonacci-Zahlen 1, 1, 2, 3, 5, 8, 13, 21, 34, … entsprechen, dann kann man sie schön nebeneinandersetzen. Skizziert man in jedem von ihnen einen Viertelkreis, dann entsteht die Fibonacci-Spirale.
Die Fibonacci-Zahlen figurieren in den spiralförmigen Strukturen an der Oberfläche von Nadelbaumzapfen oder der Ananas, im Körbchen der Sonnenblume, des Gänseblümchens und anderer Blüten. An den genannten Pflanzen kann man zwei Spiralsysteme beobachten. Linksdrehende und rechtsdrehende Spiralen. Die Zahlen der Spiralen in beide Richtungen entsprechen stets der Größe der Pflanze, oder können durch die Nachbarglieder der Fibonacci-Folge ausgedrückt werden. Bei der Sonnenblume beispielsweise sind es am häufigsten 34 Spiralen in eine und 55 Spiralen in die andere Richtung.
Interessant ist es, die Zahl der Blütenblätter von Blüten verschiedener Pflanzen zu beobachten. Sehr oft kommen Blüten vor, deren Anzahl der Blütenblätter irgendeiner Fibonacci-Zahl entspricht. Beispiele: 1 Blatt: Calla, Flamingoblume, 2 Blätter: Wolfsmilch, 3 Blätter: Schwertlilie, 5 Blätter: Vergissmeinnicht, 8 Blätter: Scharbockskraut, 13 Blätter: Sonnenhut, 21 Blätter: Wegwarte, 34 Blätter: Margerite.
Die Fibonacci-Zahlen treten oft dort auf, wo wir auch auf den goldenen Schnitt treffen. Die Rechtecke, denen wir beim Bau der Quadratspirale begegnen, sind von goldenen Rechtecken nicht zu unterscheiden.
„Die Geometrie hat zwei Schätze: Den Satz des Pythagoras und den Goldenen Schnitt.
Ersterer ist Gold wert, der zweite ähnelt eher einem Edelstein.”
Johannes Kepler
Egal, wie man den goldenen Schnitt auch ausdrückt, stets hat er eine gewisse Einfachheit und Charme an sich.
Mathematisch:
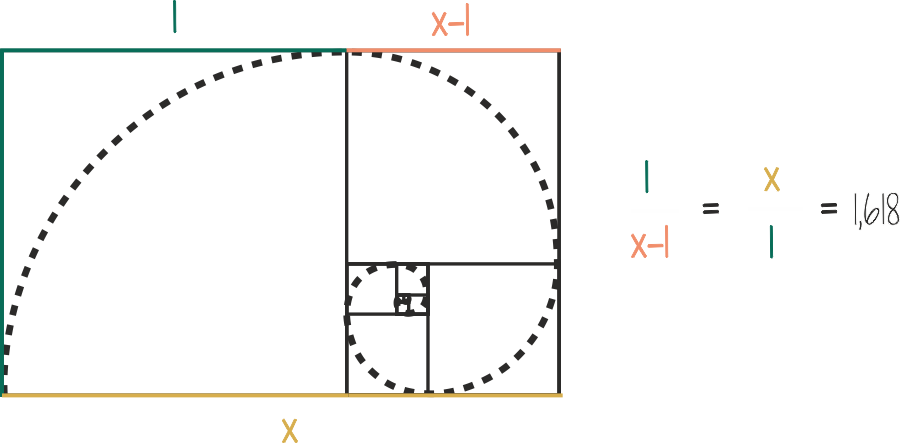
Wenn der goldene Schnitt x ist, dann gilt
x2 – x – 1 = 0,
was auch wie folgt notiert werden kann
x/1 = 1/(x-1).
In Worten ausgedrückt:
„Der Goldene Schnitt ist das Verhältnis, bei dem sich der ganze Teil zum größeren genauso verhält, wie der größere Teil zum kleineren.“
Ein gutes Beispiel für den goldenen Schnitt ist die Kreditkarte, deren Größe weltweit standardisiert ist. Sie steht im Einklang mit der Definition des goldenen Schnitts. Das goldene Rechteck ist dank seiner ausgeglichenen Gestalt eine beliebte Form – es ist weder zu lang noch zu breit.
Wie findet man heraus, ob ein Rechteck golden ist?
Lege zwei Rechtecke nebeneinander: eins im Hochformat, das zweite daneben im Querformat. Wenn du die Diagonale durch das Rechteck im Querformat ziehst und diese den oberen Eckpunkt des zweiten Rechtecks erreicht, dann sind beide golden.
Finde den goldenen Schnitt am menschlichen Körper.
Finde und überprüfe den goldenen Schnitt: