Fraktal to obiekt geometryczny o pozornie skomplikowanej strukturze.
Jego typową cechą jest samopodobieństwo, gdyż kształt fraktalny składa się z części, które są zmniejszonymi kopiami całości.
Tradycyjna geometria zajmuje się figurami idealnymi – prostymi, doskonałymi okręgami, bezbłędnymi ciałami. W świecie rzeczywistym nic takiego nie istnieje. Kamienie, drzewa, rośliny, a nawet chmury są nieregularne, ułamkowe, rozczłonkowane. Matematyka okazała się nieskuteczna przy opisywaniu świata i rzeczy, których nie stworzył człowiek, ponieważ przyroda jest nieforemna. Mimo tego próbuje to robić za pomocą tzw. fraktali.
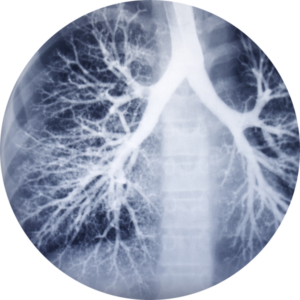
Matematyka fraktali to próba przybliżenia się do ułamkowości codziennego życia. Geometria fraktalna ma ogromne znaczenie przy opisywaniu kształtów i obiektów rzeczywistego świata. Większość prawdziwych obiektów jest zbyt skomplikowana, aby można je było opisać za pomocą geometrii euklidesowej, natomiast geometria fraktalna potrafi odzwierciedlić nawet bardzo skomplikowane struktury, takie jak na przykład sieć wodna, struktura płuc, kształt chmur czy wyładowanie elektryczne.
Płatek Kocha
Jednym z podstawowych kształtów występujących w geometrii fraktalnej jest płatek Kocha, który został po raz pierwszy opisany w 1904 roku. Na jego kształcie możemy łatwo wyjaśnić zasadę tworzenia fraktali i cechę samopodobieństwa.
Podstawą płatka jest trójkąt równoramienny.
Do środków boków tego trójkąta przyłączymy kolejne trójkąty, zmniejszone w stosunku do poprzedniego w skali 1:3.
Do tych trójkątów przyłączymy kolejne trójkąty, ponownie pomniejszone o jedną trzecią.
Powtarzając to, stopniowo otrzymamy rozczłonkowany obiekt, nazywany płatkiem Kocha.

Trójkąt Sierpińskiego

Sześciokąt Sierpińskiego

Dywan Sierpińskiego

Fraktale mają związek z ogromnymi postępami w informatyce i teorii chaosu, ale ich geometria ma swoją własną historię. Formy pokazane po lewej stronie pochodzą z początku XX wieku i początkowo uważane były za matematyczne kurioza.
Także ciało człowieka składa się z fraktali – każdy poziom powiększenia zawiera części i całości. Przykładowo płuca niewiarygodnie skutecznie wypełniają przestrzeń. Mają wiele fałd i wygięć, ich objętość jest bardzo mała, ale całkowita powierzchnia jest ogromna.
Z powodu złożonej powierzchni brokułu trudno zmierzyć jego powierzchnię. Im bliżej patrzymy na powtarzające się wzory różyczek i zwojów, tym więcej szczegółów widzimy. Metoda dodawania powtarzanych jednostek na różnych poziomach skali, widoczna na romanesco (najpiękniejsze warzywo na świecie – „zielony kalafior”), dała początek zjawisku nazywanemu „samopodobieństwem”.

Zbiór Mandelbrota

Zbiór Mandelbrota należy do najsłynniejszych obiektów współczesnej matematyki. Po raz pierwszy pojawił się dopiero w latach 80. XX wieku wraz z rozwojem techniki komputerowej i jej wykorzystywaniem w coraz dokładniejszych obliczeniach matematycznych. Chociaż zbiór Mandelbrota wygląda skomplikowanie, jego obliczenie nie jest wcale trudne i obejmuje tylko dodawanie i mnożenie.
Wzór do obliczenia zbioru Mandelbrota:
z = z2 + c
Kluczową cechą jest iteracja – prosta zasada powtarzająca się w nieskończoność. Mandelbrot stwierdził, że dla pewnych wartości liczb zespolonych z wzór rośnie w nieskończoność, ale dla innych spada do zera. Gdy przeprowadzimy to obliczenie dla wszystkich liczb zespolonych, a te, które nie dążą do nieskończoności, narysujemy na wykresie, otrzymamy zbiór Mandelbrota. Na zewnątrz są wartości z rosnące w nieskończoność, w środku są te skazane na zanik, czyli prowadzące do zera. Bez względu na to, jak obrazek przybliżymy, zobaczymy podobne kształty i nie będziemy w stanie dotrzeć do ostatniego punktu. Kształty będą się wciąż powtarzać.
Fraktale często odzwierciedlają kształty zjawisk przyrodniczych. Szczegóły zbioru Mandelbrota przypominają gwiaździste boczne ramiona olbrzymiego jeziora Nasera w Egipcie lub zapory Aquelva w Portugalii.

Każdy obiekt ma wymiar fraktalny, który jest typem statystycznej miary stopnia chropowatości. Gdy popatrzymy na jakiś obiekt, wydaje nam się niematematyczny, ponieważ widzimy całą jego złożoność. Gdy przyjrzymy się uważnie, z jakich kształtów się składa, możemy zobaczyć trójwymiarową geometrię nieustannie powtarzających się, samopodobnych obiektów. Wzory dla drzew, chmur i masywów górskich mogą tworzyć się całkowicie sztucznie na podstawie stopnia ich złożoności.





