Ein Fraktal ist ein geometrisches Objekt mit einer scheinbar komplizierten Struktur.
Seine typische Eigenschaft ist die Selbstähnlichkeit, wobei die fraktale Figur aus Teilen gebildet wird, die verkleinerte Kopien der Gesamtfigur sind.
Die traditionelle Geometrie beschäftigt sich mit idealen Figuren – absolut geraden Geraden, perfekten Kreisen, fehlerlosen Körpern. In der reellen Welt existiert nichts dergleichen. Steine, Bäume, Pflanzen, selbst Wolken sind unregelmäßig, bruchstückhaft, fragmentiert. Im Falle der Notwendigkeit, die Welt und nicht vom Menschen geschaffene Dinge zu beschreiben, stieß die Mathematik auf Grenzen, denn die Natur ist unförmig. Dennoch bemüht sie sich mit Hilfe sog. Fraktale darum.
Die Mathematik der Fraktale ist der Versuch, sich der Bruchstückhaftigkeit des Alltagslebens anzunähern. Die fraktale Geometrie ist bei der Beschreibung von Formen und Objekten des reellen Lebens von enormer Bedeutung. Die meisten tatsächlichen Objekte sind zu kompliziert, um sie mittels Euklidischer Geometrie beschreiben zu können. Die fraktale Geometrie hingegen vermag auch sehr komplizierte Strukturen zu veranschaulichen, wie zum Beispiel das Gewässernetz, die Struktur der Lunge, die Form von Wolken oder die elektrische Entladung.
Kochsche Schneeflocke
Eine der in der fraktalen Geometrie auftretenden Grundformen ist die Kochsche Schneeflocke, die erstmals im Jahr 1904 beschrieben wurde. An ihrer Form lässt sich das Prinzip der Erstellung von Fraktalen und die Eigenschaft der Selbstähnlichkeit leicht erklären.
Die Basis der Flocke ist ein gleichseitiges Dreieck.
An die Mitten der Seiten dieses Dreiecks werden weitere Dreiecke angefügt, die gegenüber dem ursprünglichen im Verhältnis 1:3 verkleinert sind.
An diese Dreiecke schließen wir weitere, wiederum um ein Drittel verkleinerte Dreiecke an.
Durch die schrittweise Wiederholung dieser Vorgehensweise erhält man eine gegliederte Figur, die als Kochsche Schneeflocke bezeichnet wird.

Sierpinski-Dreieck

Sierpinski-Sechseck

Sierpinski-Teppich

Fraktale sind mit enormen Fortschritten in der Informatik und der Chaostheorie verbunden, aber ihre Geometrie hat ihre eigene Geschichte. Die links dargestellten Formen stammen von Anfang des 20. Jahrhunderts und galten ursprünglich als mathematische Kuriositäten.
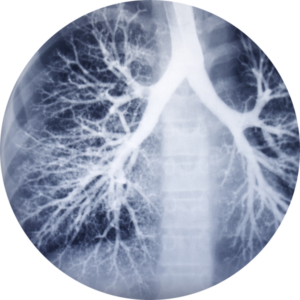
Auch der menschliche Körper besteht aus Fraktalen – jede Vergrößerungsebene enthält Details und Ganze. Beispielsweise füllt die Lunge den Raum unglaublich effektiv. Sie hat viele Falten und Kerben, deren Volumen sehr klein ist, aber ihre Gesamtoberfläche ist enorm.
Wegen der komplexen Oberfläche des Brokkoli ist die Messung seiner Fläche schwierig. Je näher man sich die sich wiederholenden Muster der Röschen und Windungen anschaut, umso mehr Details sieht man. Die Methode des Einlesens wiederholter Einheiten auf verschiedenen Ebenen des Maßstabes, wie dies am Romanesco (schönstes Gemüse der Welt – „grüner Blumenkohl“) ersichtlich ist, ließ ein Phänomen entstehen, das als „Selbstähnlichkeit“ bezeichnet wird.

Mandelbrot-Menge

Die Mandelbrot-Menge gehört zu den am häufigsten dargestellten Figuren in der modernen Mathematik. Erstmals tauchte sie in den 80er Jahren des 20. Jahrhunderts mit der Entwicklung der Computertechnik und ihrem Einsatz für immer genauere mathematische Berechnungen auf. Auch wenn die Mandelbrot-Menge kompliziert aussieht, ist ihre Berechnung überhaupt nicht schwierig und umfasst lediglich Addition und Multiplikation.
Formel für die Berechnung der Mandelbrot-Menge:
z = z2 + c
Ihre Schlüsseleigenschaft ist die Iteration – eine einfache Regel, die sich bis ins Unendliche wiederholt. Mandelbrot stellte fest, dass die Formel für bestimmte Werte komplexer Zahlen z ins Unendliche wächst, während sie für andere gegen Null sinkt. Wenn wir diese Berechnung für alle komplexen Zahlen durchführen und diejenigen, die uns nicht ins Unendliche entronnen sind, in einen Graphen eintragen, erhalten wir die Mandelbrot-Menge. Außen befinden sich die Werte z, die gegen das Unendliche wachsen, innen sind die Werte gefangen, die zum Untergang verurteilt sind, also Richtung Null gehen. Ungeachtet dessen, wie wir das Bild annähern, sehen wir stets ähnliche Formen und können zu keinem Endpunkt gelangen. Die Formen wiederholen sich ständig.
Fraktale spiegeln häufig die Formen von Naturphänomenen wider. Die Details der Mandelbrot-Menge ähneln den sternartigen Seitenarmen des riesigen Nassersees in Ägypten oder des Alqueva-Sees in Portugal.

Jedes Objekt hat eine fraktale Dimension, die eine Art statistisches Rauheitsmaß ist. Sieht man sich ein Objekt an, erscheint es einem nichtmathematisch, weil man seine ganze Komplexität sieht. Wenn man sich genau anschaut, aus welchen Formen es sich zusammensetzt, kann man die dreidimensionale Geometrie sich ständig wiederholender selbstähnlicher Objekte sehen. Die Formeln für Bäume, Wolken und Gebirgszonen können anhand des Maßes ihrer Komplexität völlig künstlich gebildet werden.





