Fractal is a geometrical object with seemingly complicated structure.
A typical feature is self-similarity, where a fractal pattern is formed from parts, that are scaled down copies of the entire pattern.
Traditional geometry deals with ideal shapes – direct lines, perfect circles, flawless objects. There is no such thing in the real world. Stones, trees, plants, even clouds are irregular, fragmentary, fragmented. In the need to describe the world and things not created by a human, mathematics came across because the nature is shapeless. Nevertheless, there is effort thanks to so called fractals.
Fractal mathematics is an attempt to approach the fragmentation of everyday life. Fractal geometry is of great importance in describing shapes and objects of the real world. Majority of the real objects is too complex to be described with Euclidean geometry, while fractal geometry can depict even very complex structures, such as water network, lung structure, shape of clouds or electric shock.
Koch snowflake
One of the basic shapes occurring in fractal geometry is Koch’s snowflake, that was first described in 1904. We can easily explain the principle of creating fractals and the feature of self-similarity on its shape.
The base of the snowflake is an equilateral triangle.
To the centres of the sides of this triangle we add next triangles, reduced compared to our previous triangle in the ratio 1 : 3.
We connect more triangles reduced by one third to those triangles.
By gradually repeating the procedure we obtain a segmented pattern called the Koch snowflake.

Sierpiński triangle

Sierpiński hexagon

Sierpiński carpet

Fractals are associated with enormous advances in computer science and chaos theory, but their geometry has its own history. The forms depicted on the left come from the early 20th century and were originally considered mathematical curiosities.
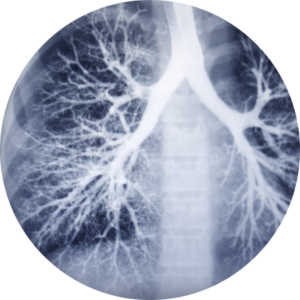
Even human body is made up of fractals – every level of magnification contains details and wholes. For example, lungs fill space unbelievably efficiently. They have many folds and ridges, their volume is very small, but their overall surface is enormous.
Due to the complex surface of a broccoli, it is difficult to measure its surface area. The closer we look at the repeating patterns of roses and threads, the more details we see. The method of reading repeated units at different levels of scale, as it appears on the Romanesque (the most beautiful vegetable in the world – „green cauliflower “), gave rise to a phenomenon called self-similarity.

Mandelbrot set

Mandelbrot set belongs to the most often depicted images in modern mathematics. Its first appearance was in the 1980s with development of computer technology and its use for increasingly accurate mathematical calculations. Even though Mandelbrot set looks complicated, its calculation is not difficult at all, and only contains addition and multiplication.
Formula for calculating the Mandelbrot set:
z = z2 + c
The key feature is iteration – a simple rule repeating itself indefinitely. Mandelbrot discovered, that for certain values of complex numbers, the formula increases to infinity, but for others it decreases to zero. If we perform this calculation for all complex numbers and draw the ones that did not run to infinity, we get the Mandelbrot set. Outside there are values ascending to infinity, inside are those doomed to extinction, thus heading to zero. No matter how we zoom in on the image, we will see similar shapes and we will not be able to get to the end point. The shapes will keep repeating.
Fractals often reflect shapes of natural phenomena. Details of Mandelbrot set are reminiscent of the star-shaped side arms of the giant Lake Nasser in Egypt or Lake Aquelva in Portugal.

Each object has a fractal dimension, which is a type of statistical degree of roughness. When we look at an object, it seems not mathematical, because we see all its complexity. If we look closely at the shapes it consists of, we can see the three-dimensional geometry of constantly repeating, self-similar objects. Formulas for trees, clouds, and mountain ranges can be created completely artificially based on the degree of their complexity.





