VOM ANTRITT UNSERER REGIERUNG WÄCHST DIE WIRTSCHAFT 2X SCHNELLER!!!
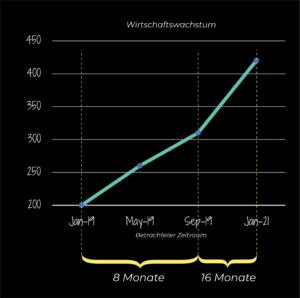
Wirklich? Etwas stimmt nicht an der x-Achse.
Wenn man auf der x-Achse nicht gleich große Zeitabschnitte verwendet (z. B. Monate), kann das die Form des Graphen deutlich verändern. Da ein Manipulator im linken Graphen 8 Monate der alten Regierung auf einen doppelt so langen Abschnitt in die Breite gezogen hat, wie die 16 Monate seiner Regierung, erscheint das Wirtschaftswachstum steiler. Ist das wahr? Die neue Regierung erreichte in Wirklichkeit einen Anstieg um 210 Punkte, genau wie die alte Regierung, aber innerhalb eines doppelt so langen Zeitraums. Und damit würde sie sich wohl kaum rühmen.
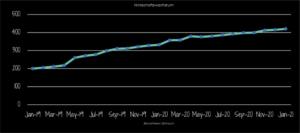
SO FÜRCHTERLICH SIND UNSERE GEWINNE ZURÜCKGEGANGEN. WIR MÜSSEN ENTLASSEN!!!
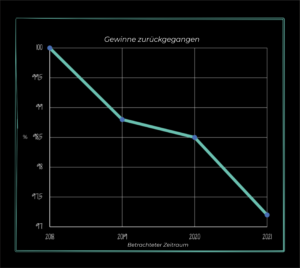
Wirklich? Versuchen wir einmal die y-Achse von 0 bis 100 % zu verwenden.
Wenn jemand betonen will, wie sehr ein Wert im Laufe der Jahre z. B. abnimmt, verwendet er den ersten Graphen. Wenn nicht, dann den zweiten. Wobei beide von denselben Daten ausgehen und beide im Prinzip richtig sind. Es geht jedoch um den Kontext. Manchmal kann eine Differenz von 2 % wichtig sein. Manchmal aber auch nicht, und ein richtiger Manipulator kann sein Publikum durch die Verwendung des ersten Graphen gewiss leichter erschrecken.
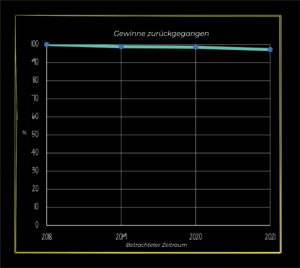
Was will mir dieses Bild sagen?
Wenn dir das nächste Mal jemand einen Graphen zeigt, schau nicht nur auf die Striche und Kurven. Kontrolliere:
Achsen, Zahlen, Skalen und Kontext
GLOBALE ERWÄRMUNG GIBT ES DOCH NICHT!
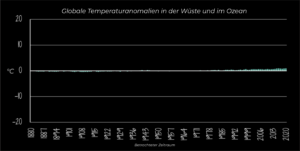
Sehen wir uns das einmal näher an.
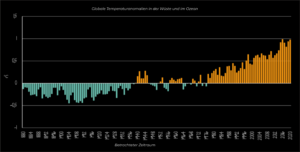
Die Situation kann sich je nach Kontext auch umkehren. Am oberen Graphen erscheint es, dass sich die globale Temperatur im Laufe von 140 Jahren nur ein kleines bisschen erhöht hat. In einem Kontext, in dem eine Änderung um einen Grad das gesamte Ökosystem des Planeten stören und aus einem Großteil des Planeten unbewohnbares Gebiet machen kann, sollte man sich die Daten jedoch näher ansehen. Deshalb hat der untere Graph eine viel größere Aussagekraft.
Wie lügt die Statistik?
Stell dir zwei Krankenhäuser vor – X und Y.
Krankenhaus X heilte 900/1000 (90 %) und Y heilte 800/1000 (80 %) seiner Patienten.
Für welches Krankenhaus sollte ich mich also entscheiden?
Krankenhaus X hat mehr Patienten geheilt. Also gehe ich dorthin!
Wirklich?
Schwerkranke: Krankenhaus X heilte
30 / 100 …. 30 %
Krankenhaus Y heilte
210 / 400 …. 52,2 %
Leichtkranke: Krankenhaus X heilte
870 / 900 …. 96,6 %
Krankenhaus Y heilte
590 / 600 …. 98,3 %
Das kommt bei mir raus!!! Hmmm …
Hier ist die Erklärung
Das nennt man Simpson-Paradoxon.
Das Problem besteht darin, dass wir zwei unterschiedliche Gruppen miteinander verbunden haben: Schwerkranke und Leichtkranke.
Wenn man etwas derart beurteilen will, muss man zunächst darüber nachdenken, ob man im Kontext dessen, was man untersucht, nicht Gruppen von Menschen (Subjekten) mit allzu unterschiedlichen Eigenschaften verbindet (z. B. Gesundheitszustand alter und junger Menschen, Preise von Häusern und Wohnungen u. Ä.).
| Schwerkranke | Leichtkranke | Insgesamt | |
| Krankenhaus X | 30/100 (30 %) | 870/900 (96,6 %) | 900/1000 (90 %) |
| Krankenhaus Y | 210/400 (52,5 %) | 590/600 (98,3 %) | 800/1000 (80 %) |





