NUMBERS IN NATURE
Fibonacci sequence / numbers
Fibonacci numbers are perhaps the most famous sequence named after Fibonacci or Leonardo of Pisan. Each number in this sequence is the sum of the two preceding numbers, so for example
2 = 1 + 1; 3 = 1 + 2; 5 = 2 + 3 and so on.

It is interesting to monitor the number of petals of flowers of different plants. Flowers with a number of petals of some Fibonacci number are very common. Examples: 1 slice: calla, anthurium, 2 slices: euphorbia, 3 slices: iris, 5 slices: forget-me-not, 8 slices: celandine, 13 slices: shaggy, 21 slices: chicory, 34 slices: daisy.
Fibonacci numbers often occur where we meet the golden ratio. The rectangles we encounter in the construction of the square spiral are indistinguishable from the golden rectangles.
“Geometry has two great treasures; one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel.”
Johannes Kepler
No matter how we express the golden ratio, it always has a certain simplicity and charm.
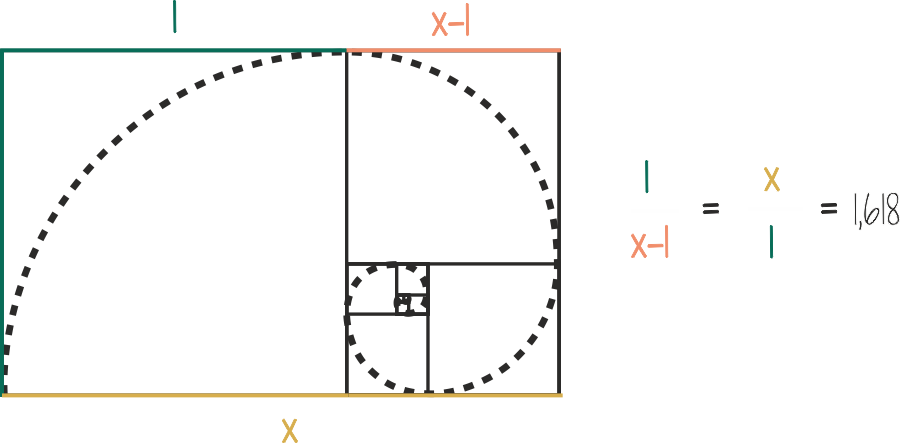
Mathematically:
If the golden ratio is x, then
x2 – x – 1 = 0,
which can be recorded as
x/1 = 1/(x-1).
Expressed in words:
„The golden ratio is the ratio at which the whole is to the longer part as the longer part is to the shorter part.„
A good example of the golden ratio is a credit card whose size is standardized worldwide. It is in line with the definition of the golden ratio. The golden rectangle is a popular shape due to its balanced appearance – it is neither too long nor too wide.
A good example of the golden ratio is a credit card whose size is standardized worldwide. It is in line with the definition of the golden ratio. The golden rectangle is a popular shape due to its balanced appearance – it is neither too long nor too wide.
How to tell if a rectangle is golden?
Place two rectangles next to each other: one portrait, the other landscape. If you fold the diagonal to the width of the rectangle and it reaches the top of the second rectangle, then both are gold.
Find the golden ratio on the human body.
Find and verify the golden ratio:






