Osová souměrnost (Zrcadlení)
Objekt můžeme nazvat osově souměrným, když ho umíme rozdělit na dvě zrcadlově stejné části – dvě části stejné velikosti a tvaru. Přímka, která rozděluje objekt, se nazývá OSA SOUMĚRNOSTI.
Zrcadlení podle osi

Čtverec má 4 osy souměrnosti.
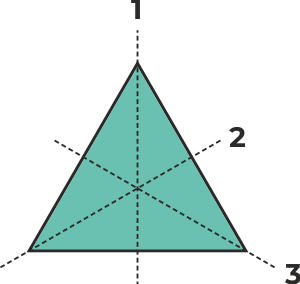
Rovnostranný trojúhelník má 3 osy souměrnosti.
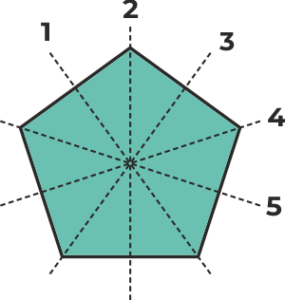
Pravidelný pětiúhelník má 5 os souměrnosti.

Tento tvar má 1 osu souměrnosti. Všechny odpovídající části jsou ve stejné vzdálenosti od osy souměrnosti.
Přestože je symetrie velmi komplikovaná a propracovaná, je to jeden z prvních matematických konceptů, které děti pochopí. Osovou souměrnost nazýváme i zrcadlový obraz. Vzpomeň si na ni, když se příště podíváš do zrcadla.
Možná tě překvapí, že většina lidí nemá souměrný obličej.
Rotační symetrie (Otočení)
Objekt má rotační symetrii, pokud se po pootočení o určitý úhel kolem centrálního bodu vrátí do své původní podoby.
Otočení kolem středu
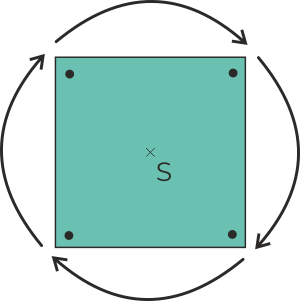
Čtverec má 4-násobnou rotační symetrii. Vrátí se do původního tvaru otočením o 90°.
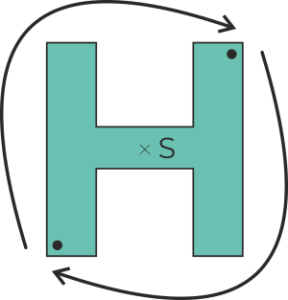
Písmeno H má 2-násobnou rotační symetrii. Vrátí se do původního tvaru otočením o 180°. – Otočení o 180° se také nazývá středová souměrnost.
Symbol recyklace má 3-násobnou rotační symetrii. Vrátí se do původního tvaru otočením o 120°.

Každý pravidelný n-úhelník má n násobnou rotační symetrii.
Hvězdice je skvělým příkladem rotační symetrie i osové souměrnosti. Má 5-násobnou rotační symetrii a 5 os souměrnosti.
Představ si, že najdeš hvězdici na pláži. Když ji otočíš o jednu pětinu, bude vypadat stejně.
Existuje dokonale souměrný tvar?






