Stínohra je starodávná forma vyprávění a zábavy, která využívá ploché figurky (stínové loutky), které jsou drženy mezi zdrojem světla a průsvitnou obrazovkou nebo plátnem.
Stínové divadlo má dlouhou historii a je populární v různých kulturách jihovýchodní Asie, Číny i Evropy. Princip stínohry se rozvinul s rozvojem fotografie do promítaní diapozitivů a nakonec do kinematografie. Společným principem těchto médií je kreativní využití světla a projekční plochy ve spojení s tvorbou obrazu na základě průsvitnosti.
Na naší didaktické pomůcce si můžeš vyzkoušet princip stínohry. Pozoruj, v jaké vzdálenosti je třeba umístit předměty stejného tvaru a různé velikosti tak, aby jejich stín byl stejně velký. Můžeš také kombinovat více tvarův různé vzdálenosti a vytvořit tak složité panorama.
Pozorování stínů v přírodě nám může přinést zajímavé informace. Například řecký učenec Aristoteles experimentálně odvodil kulový tvar Země z pozorování stínu Země při zatmění Měsíce. Podobný princip jako u stínohry – založený na lineární funkci – umožňuje lesníkům změřit výšku stromů nebo zeměměřičům určit výšku budov jen pomocí měření úhlů z přesných optických pozorování. Více o této aplikaci se dozvíte u pomůcky Talesův teorém
Lineární funkce je funkce, jejíž funkční hodnota se mění úměrně nezávisle proměnné.
Lineární funkce na množině reálných čísel je každá funkce , která je dána předpisem:
ƒ : y = ax + b
kde a,b ∈ R. Definičním oborem jsou všechna reálná čísla Dy = R .
Grafem lineární funkce je přímka. Důležitými body grafu lineární funkce jsou průsečíky přímky se souřadnicovými osami x a y.
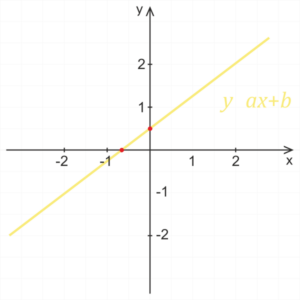
Viv koeficientů a, b na graf lineární funkce.
Vliv koeficientu a
Pro kladný koeficient a je lineární funkce rostoucí, pro záporný koeficient a je funkce klesající. Čím větší je absolutní hodnota koeficientu a, tím je graf funkce více přimknutý k ose y. Jestliže je absolutní hodnota koeficientu a menší než jedna, pak s klesající absolutní hodnotou koeficientu a se graf funkce stále více přimyká k ose x.
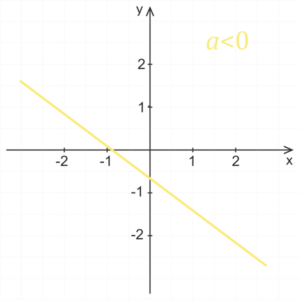
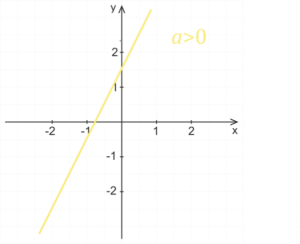
Vliv koeficientu b
Graf funkce protíná osu y v bodě o ypsilonové souřadnici rovné koeficientu b.
a=0
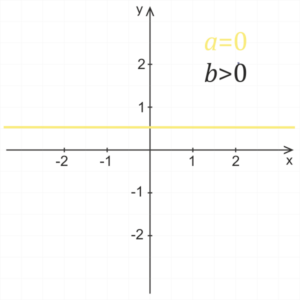
Pro nulový koeficient a získáváme předpis y=b, což je předpis konstantní funkce.
b=0
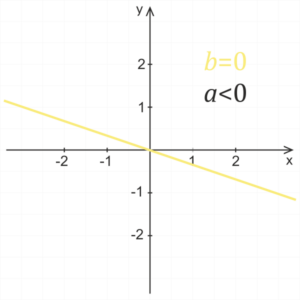
Pro nulový koeficient b získáváme předpis y=ax, což je předpis lineární funkce, jejíž graf prochází počátkem soustavy souřadnic.
Výpočet průsečníku grafu lineární funkce y=ax+b s osou x
Každý bod ležící na ose x má ypsilonovou souřadnici rovnou nule, po dosazení y = 0 do předpisu lineární funkce získáme lineární rovnici a jejím vyřešením získáme požadovaný průsečík:
ax+b=0 x=-b/a;a≠0
Výpočet průsečníku grafu lineární funkce y=ax+b s osou y
Každý bod ležící na ose y má ixovou souřadnici rovnou nule, po dosazení x = 0 do předpisu lineární funkce získáme ypsilonovou souřadnici požadovaného průsečíku:
y=0x+by= b






