Kvadratická funkce je funkce, jejíž funkční hodnota se mění úměrně druhé mocnině nezávisle proměnné.
Kvadratická funkce na množině reálných čísel je každá funkce f, která je dána předpisem:
f: y=ax2 +bx+c
kde a, b, c∈R ∧a≠0. Definičním oborem jsou všechna reálná čísla Dy =R.
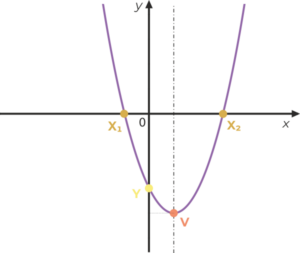
Grafem kvadratické funkce je křivka, která se nazývá parabola. Důležitými body paraboly jsou její vrchol V a průsečíky paraboly se souřadnicovými osami x a y. Graf je souměrný podle osy paraboly, která je rovnoběžná s osou y a prochází jejím vrcholem.
V – vrchol paraboly
X1 , X2 – průsečíky s osou x
Y – průsečík s osou y
Vliv koeficientů a, b, c na graf kvadratické funkce.
Vliv koeficientu a
Pro kladný koeficient a je graf kvadratické funkce konvexní („otevřený“ nahoru), pro záporný koeficient a je graf kvadratické funkce konkávní („otevřen“ dolů). S rostoucí absolutní hodnotou koeficientu a je parabola více „přimknutá“ ke své ose.
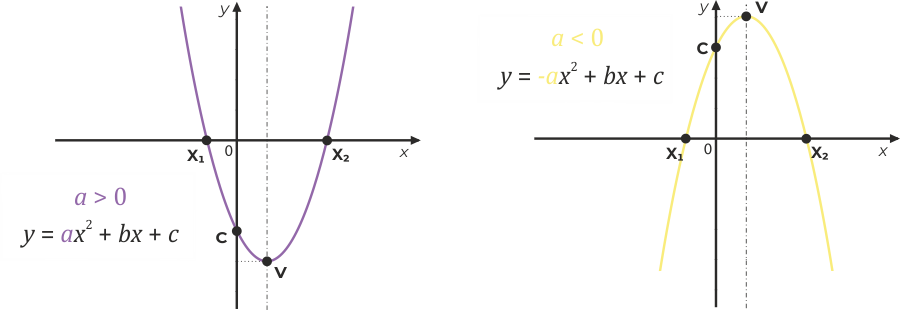
Vliv koeficientu b
Koeficient b souvisí se směrnicí tečny k parabole v jejím průsečíku s osou y. Budeme-li se na tuto tečnu dívat jako na jinou funkci, např. g, pak předpis této funkce je g: y = bx + c. Je-li koeficient b roven nule, pak vrchol paraboly leží na ose y.
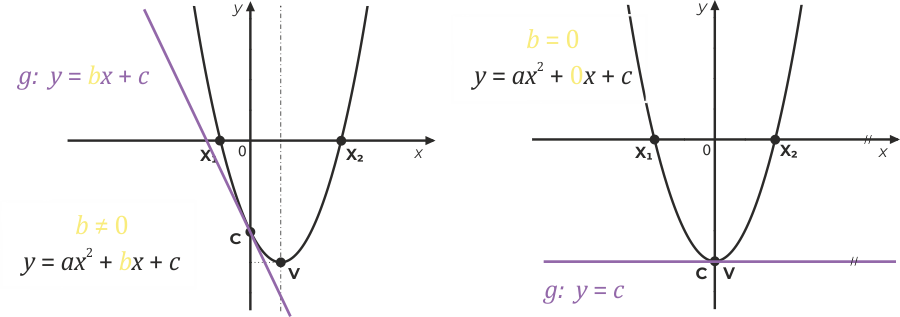
Vliv koeficientu c
Graf funkce protíná osu y v bodě o ypsilonové souřadnici rovné koeficientu c.
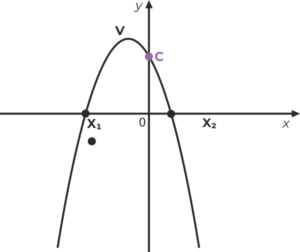
Výpočet průsečíků grafu kvadratické funkce y=ax2 +bx+c s osou x
Každý bod ležící na ose x má ypsilonovou souřadnici rovnu nule, po dosazení y = 0 do předpisu kvadratické funkce získáme kvadratickou rovnici, jejím vyřešením získáme požadované průsečíky:
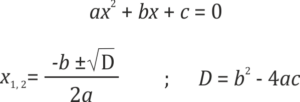
Ve speciálních případech lze k určení souřadnic průsečíků využít rozkladu kvadratického trojčlenu na součin kořenových činitelů.
Výpočet souřadnic vrcholu paraboly kvadratické funkce y=ax2 +bx+c
Obecně získáme souřadnice vrcholu snadno pomocí vzorce:
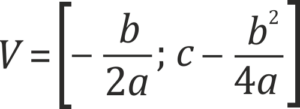
tyto vzorce získáme tzv. doplněním předpisu funkce na čtverec a několika algebraickými úpravami. Doplněním na čtverec konkrétní zadané funkce získáme konkrétní souřadnice vrcholu i bez znalosti vzorců. Ke zjištění souřadnic vrcholu lze také využít průsečíky paraboly s osou x nebo první derivace funkce.






