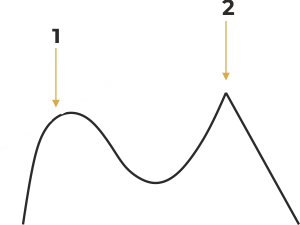
Derivace je důležitý pojem matematické analýzy a základ diferenciálního počtu. Vznikl v 17. století díky objevům Newtona a Leibnize při řešení geometrických a fyzikálních problémů. Má významnou roli při určování průběhu funkce, protože derivace popisuje změnu hodnoty funkce v poměru ke změně nezávisle proměnné. V případě dvourozměrného grafu funkce f(x) je derivace této funkce v libovolném bodě rovna směrnici tečny tohoto grafu. Tečna svírá úhel s osou x a tangens tohoto úhlu nazýváme směrnicí tečny. Derivaci funkce v bodě lze s dostatečnou přesností aproximovat právě jako tuto směrnici tečny. Je-li v bodě x křivka rostoucí, bude její derivace >0 a je-li klesající, bude derivace <0.
Pokud v bodě existuje derivace, je jediná. Žádná funkce nemá v jednom bodě více derivací. Má-li funkce v bodě derivaci, pak je funkce v tomto bodě spojitá. Pokud je ovšem funkce spojitá v daném bodě, neznamená to, že je zde derivovatelná. Typickým příkladem je funkce f(x) = |x|. Graf je do špičky, a nelze vypočítat směrnici tečny v této špičce.
Občas potřebujeme znát tzv. druhou derivaci. Nejedná se o nic složitého, prostě funkci zderivujeme jednou a poté výsledek zderivujeme ještě podruhé. Značíme to dvěma čárkami: f“(x) = (f'(x))‘.
1.Derivace – směrnice tečny
2.Derivace neexistuje
Družice obíhající Zemi se pohybují po kružnici, dráhy po nichž se pohybují některé komety v sluneční soustavě jsou velmi blízké elipsám nebo parabolám.
Minimum a maximum funkce
Nalezení bodů, kde funkční hodnota nabývá buď maxima nebo minima – tzv. extrémů funkce, je důležité pro pochopení průběhu funkce a také pro řešení složitých úkolů jako je např. nelineární regrese (optimalizace procesů). Extrémy lze snadno nalézt pomocí derivace funkce, protože v těchto bodech musí být derivace nulová. Tato úloha se velice podobá člověku vystupujícímu v mlze na kopec – jak zjistíte že se nacházíte na jeho vrcholu?
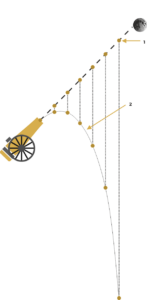
Od výstřelu z děla až do vesmíru
Dráhu tělesa pohybujícího se v gravitačním poli je možné aproximovat kuželosečkami. Družice obíhající Zemi se pohybují po kružnici, dráhy po nichž se pohybují některé komety v sluneční soustavě jsou velmi blízké parabolám. Rychlost potřebná k překonání gravitačního působení kosmického tělesa se nazýva Kosmická rychlost.
1. kosmická rychlost označuje kruhovou rychlost v gravitačním poli Země:
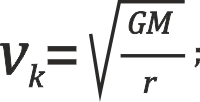
kde vk je rychlost, G gravitační konstanta, M hmotnost obíhaného tělesa a r vzdálenost středů obou těles.
2. kosmická rychlost, neboli úniková rychlost, je minimální rychlost kterou se musí těleso v gravitačním poli jiného tělesa pohybovat, aby mohlo toto gravitační pole opustit. Obíhající těleso se při ní pohybuje po parabolické trajektorii:
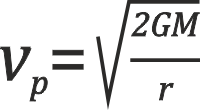
3.kosmická rychlost je úniková rychlost z gravitačního pole Slunce. Pro její velikost tedy platí vztah pro 2. únikovou rychlost, do kterého za hmotnost dosazujeme hmotnost Slunce. Těleso se při ní pohybuje po hyperbolické trajektorii.
Při započítání vlivu odporu vzduchu se tělesa (dělová koule, vržený kámen) pohybují po tzv. balistické křivce.
Balistická křivka je prostorová křivka, kterou opisuje těleso vržené či vystřelené blízko zemského povrchu obvykle směrem šikmo vzhůru. Kromě tíhového zrychlení na něj působí i aerodynamické síly. Na dráze letu tělesa jsou tři význačné body – bod výstřelu, vrchol dráhy a bod doletu.