Jak lze změřit objekt, pokud nedosáhneš metrem na jeho vrchol?
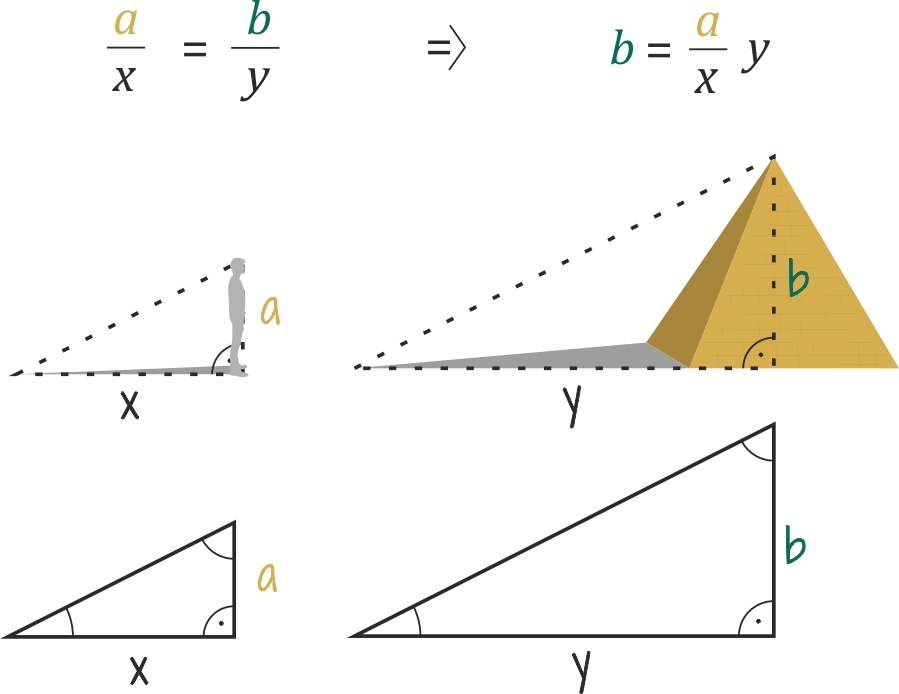
Odpověď zní: Pomocí podobnosti pravoúhlých trojúhelníků. Na tento trik přišli lidé už před tisíci lety. Jako první problém vyřešil starořecký matematik Thales, když chtěl znát výšku Velké pyramidy.
Thaletovo tělo a stín tvoří dvě strany pomyslného pravoúhlého trojúhelníku. V tomto typu trojúhelníku má jeden úhel 90° a zbývající dva dohromady 90°.
Sluneční paprsky jsou víceméně rovnoběžné, což znamená, že světlo dopadá na Thalese i pyramidu pod stejným úhlem.
Bok pyramidy je šikmý. Chceme-li dostat pomyslný trojúhelník, musíme k délce stínu připočítat délku poloviny základny.
Pokud jsou dva úhly v trojúhelníku stejné, tak musí být stejné i dvě strany.
A tedy … když sluneční paprsky dopadaly pod úhlem 45°, Thales věděl, že jeho stín má stejnou délku jako je jeho výška.
A tedy … stín pyramidy plus polovina základny má stejnou délku jako výška pyramidy.
A tedy … pokud a = a , tak b = b
Později matematici Thalesovu myšlenku rozvinuli a uvědomili si, že objekty lze změřit pomocí trojúhelníků v jakémkoli úhlu sklonu. Protože oba stíny by vytvořily podobné trojúhelníky – trojúhelníky, které mají stejné úhly a proporce, ačkoli mají jinou velikost.
A tedy platí: